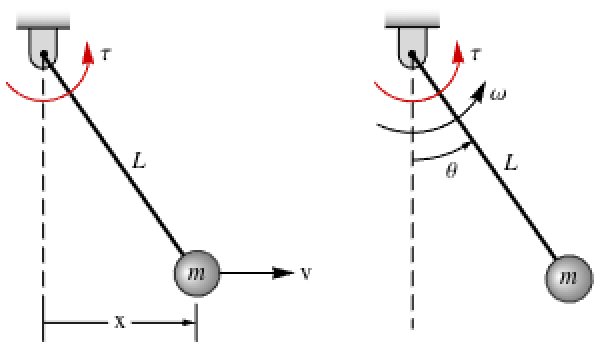
Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

StateSpaceTransform

StateSpaceTransform[sys,{p,q}]

使用矩阵 p 和 q，变换状态空间模型 sys.

StateSpaceTransform[sys,{{x₁p₁[z],…},{z₁q₁[x],…}}]

使用变量转换 {x₁p₁[z],…} 和 {z₁q₁[x],…} 进行转换.

更多信息和选项

StateSpaceTransform 返回经过变换的模型，其中状态变量已经变换. 变换可以是相似度、等价或者严格等价变换.
系统 sys 可以是一个标准或描述符 StateSpaceModel、 AffineStateSpaceModel 或者 NonlinearStateSpaceModel.
对于标准 StateSpaceModel[{a,b,c,d}]，原始和变换系统的关系由变换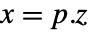表示. 相应的方程由下面给出：
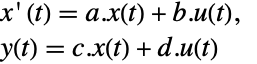
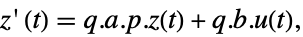
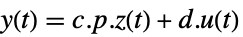
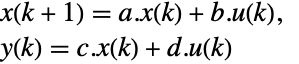
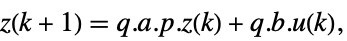
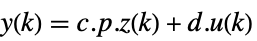
通常 p 和 q 是逆矩阵，在这种情况i型啊，变换是相似度变换. p 和 q 的下列默认值用于标准 StateSpaceModel 变换：
p 或者 {p,Automatic} {p,Inverse[p]}

{Automatic,q} {Inverse[q],q}
对于描述器 StateSpaceModel[{a,b,c,d,e}]，原始和变换系统之间的关系用变换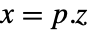表示，而相应的方程由下面给出：
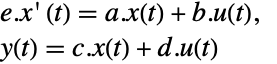
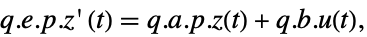
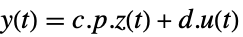
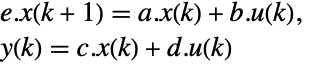
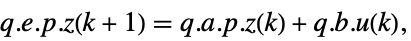
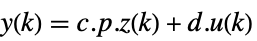
通常 p 和 q 是可逆矩阵，但不是逆矩阵，这种情况下，变换是一个等价变换. 下面默认值用于描述器 StateSpaceModel 变换：
p 或者 {p,Automatic} {p,IdentityMatrix[n]}

{Automatic,q} {IdentityMatrix[n],q}
对一个 AffineStateSpaceModel[{a,b,c,d},x] 和有 j 雅可比矩阵 D[p[z],{z}] 的 NonlinearStateSpaceModel[{f,g},x,u]，初始和变换后系统通过变换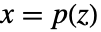相连接，并且响应方程如下给出：
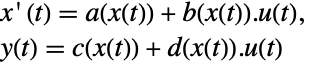
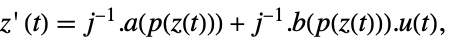
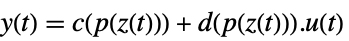
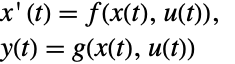
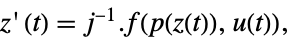
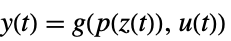
典型地， p[z] 和 q[x] 互逆，这种情况下变换是可逆映射.
{{x₁->p₁[z],…},{z₁,…}} 如果需要计算 q[x]

{Automatic,{z₁->q[x],…}} 计算 p[z]
当变量变换矩阵 {p,q} 被给出，所得系统与输入是相同类型的. 非线性状态空间模型的情况下，取它们来表示变换规则 {{x₁->p〚1〛.z,…},{z₁->q〚1〛.x,…}}.
当变量变换规则 {{x₁->p₁[z],…},…} 被给出，所得系统总是 AffineStateSpaceModel 或 NonlinearStateSpaceModel.
StateSpaceTransform 接受选项 DescriptorStateSpace.

范例

打开所有单元关闭所有单元

基本范例 (1)

相似变换：

使用矩阵对：

范围 (15)

线性变换 (10)

相似变换 :

指定矩阵对：

将变换指定为 :

描述器系统的相似变换：

描述器系统的等价变换：

相应的矩阵对指定：

获取等价描述器系统，其中状态方程提前乘以矩阵 q：

新状态就是旧状态，即 :

对于描述器系统，具有可逆 p 和 q 的变换给出等价系统：

原始系统：

不可逆的 p 或 q 给出有受限等价的系统：

在矩阵变换下，线性离散系统时间与连续时间系统的行为类似：

根据变换一个 AffineStateSpaceModel：

按照新变量 z 来指定变换：

指定变换为：

用变量：

指定变换及它的逆：

根据变换 NonlinearStateSpaceModel：

按照新变量 z：

根据逆变换：

变换和它的逆：

对于正交矩阵，可使用 Transpose，而不是 Automatic 或者 Inverse:

Nonlinear Transformations: (5)

StateSpaceModel 的非线性变换：

AffineStateSpaceModel 的非线性变换：

NonlinearStateSpaceModel 的非线性变换：

指定一个非线性变换和它的逆：

只在工作点被指定的时候需要非线性变换的逆：

推广和延伸 (2)

非正交方阵选择一个子系统：

相应的矩阵对：

对非线性变换，分隔逆指定选出一个子系统：

完备系：

选项 (1)

DescriptorStateSpace (1)

视标准 StateSpaceModel 为广义系统：

它给出与显式广义规范相同的结果：

相似的结果也可以通过逆变换获取：

应用 (6)

一个获取单输入系统的能控相伴型的函数：

一个获取单输出系统的能观测相伴型的函数：

对状态重新排列：

将一个笛卡尔坐标中的简单球摆模型转换为极坐标：

在笛卡尔坐标中的模型：

在极坐标中的模型：

应用一个直接正交变换于一个永久磁铁步进电机模型：

应用直接正交变换于电流和：

也应用直接正交变换于输入电压：

将飞行器运动方程从体坐标转化到风轴：

属性和关系 (8)

输出相应在相似度转化下不变：

相似的系统有完全相同的传递函数：

在相似度变换下，特征值（因此，稳定性）是不变的：

在相似变换下，能控性和能观测性是不变的：

Hankel 奇异值在相似度变化下不变：

系统模型分解全部使用状态转化：

基于 ControllabilityMatrix 的 ControllableDecomposition：

基于 ObservabilityMatrix 的 ObservableDecomposition：

基于 ObservabilityGramian 的 InternallyBalancedDecomposition：

基于 JordanDecomposition 的 JordanModelDecomposition：

KroneckerModelDecomposition:

通过坐标转换的线性化也是与使用 StateSpaceTransform 相关的：

状态转化是反馈线性化的中间步骤：

应用反馈和状态转换来获取变换系统：

"TransformedSystem" 属性给出相同的结果：

可能存在的问题 (2)

变换矩阵必须是标准正交的或者可逆的：

该矩阵既不是标准正交的，也不是可逆的：

如果有多个反解的话，只有一个被选定：

有三个反解：

选出期望的反解：

顶部