StructuralImportance

StructuralImportance[rdist]

ReliabilityDistribution rdist の全成分の構造重要度を与える．

StructuralImportance[fdist]

FailureDistribution fdist の全成分の構造重要度を与える．

StructuralImportance[bexpr,{x1,x2,…}]

ブール式 bexpr の成分 x1, x2, …の構造重要度を与える．

詳細

  • StructuralImportanceはBirnbaumの構造重要度としても知られている．
  • 成分 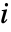の構造重要度は成分 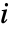が動いている系の状態の割合のことである．ただし，成分 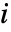が故障すると系が故障するものとする．
  • StructuralImportance[fdist]およびStructuralImportance[rdist]について，結果は rdist あるいは fdist の分布リストにおける成分順で返される．
  • StructuralImportance[bexpr,{x1,x2,…}]についての結果は{x1,x2,…}の順で返される．
  • StructuralImportance[bexpr,…]はUnateQ[bexpr]がTrueの場合に定義される．

例題

すべて開くすべて閉じる

例  (4)

直列接続された2つの成分：

結果はReliabilityDistributionにおける分布リストと同じ順で返される：

並列接続された2つの成分：

寿命分布なしに構造関数を直接使う：

故障の木に基づいたモデリングを使って系を定義する：

スコープ  (18)

ブール式モデル  (5)

並列構造では両方の成分の構造重要度が等しい：

直列構造の構造重要度：

2アウトオブ3のネットワーク中の成分の構造重要度：

混合系の重要度：

混合系の重要度：

ReliabilityDistributionモデル  (7)

並列接続の2つの成分：

どちらの成分も等しく重要である：

直列接続の2つの成分：

重要度は等しい：

3つの成分のうち2つが動かなければならない系：

成分は等しく重要である：

単純な混合系：

成分 がより重要である：

1つの成分と並列接続されている直列接続の系：

単一の成分 がより重要である：

分布が異なる2つの成分と並列に接続された1つの成分：

時間のある1点における重要性尺度を厳密な結果として求める：

機械精度による結果：

段階を追って系をモデル化して部分系の重要性尺度を得る：

FailureDistributionモデル  (6)

2つの基本事象のどちらもが頂上事象に繋がる：

2つの事象の重要度は等しい：

基本事象の両方がともに起った場合にのみ頂上事象に繋がる：

連続事象の重要度は等しい：

基本事象の分布が等しいボーティングゲート：

事象の構造重要度は等しい：

AndゲートとOrゲートの両方がある単純な系：

基本事象 が最も重要である：

AndゲートとOrゲートの両方がある単純な系：

重要度を計算する：

部分系の重要度尺度を得るために段階を追って系をモデル化する：

アプリケーション  (4)

ある町の2つの点が水道管 のネットワークで繋がれている．水の供給を維持するために最も重要な水道管を求める：

水道管 が最も重要である：

航空機の離陸時の故障を引き起こす確率が最も高い成分は何かを分析する．格納扉は電動・手動のどちらで開けることもできる：

2つの燃料ポンプを動かすためには動力が必要である：

さらに2つのポンプを信頼できる電池を使って動かすことができる．したがって次の燃料移送構造となる：

航空機の除氷装置と燃料の収蔵タンクも必要である：

重要度を計算する：

除氷装置と燃料の収蔵タンクの構造重要度が最も高い：

StructuralImportanceはBanzhaベキ指数とも呼ばれ，投票手続きの結果を変える確率を測る．地区と投票数が次の通りの郡委員会について考える：

多数になる地区の投票数のすべての組合せを求める：

多数を達成するためのブール式：

Oyster Bay，Glen Cove，Long Beachの結果はいずれもその地区だけでは投票結果を変えられない：

1804年の合衆国大統領選挙における各州のBanzhafベキ指数を計算する：

それぞれの州の人口と比較する：

人口は内側の円グラフ，ベキ指数は外側の円グラフで表されている：

人口とベキ指数のプロット：

ベキ指数を合衆国に加入した年月日と比較する：

特性と関係  (4)

構造重要度は寿命分布には依存しない：

結果は分布母数のいずれも含んでいない：

これは分布なしの指定に等しい：

構造重要度は成分の確率がのBirnbaumImportanceである：

無関係な成分は他の成分の重要度に影響しない：

無関係な成分の重要度は0である：

ReliabilityDistributionにおける bexpr の構造需要度はFailureDistributionにおける bexpr に等しい：

おもしろい例題  (1)

通常の系の構造のすべての重要性尺度を示す：

Wolfram Research (2012), StructuralImportance, Wolfram言語関数， https://reference.wolfram.com/language/ref/StructuralImportance.html.

テキスト

Wolfram Research (2012), StructuralImportance, Wolfram言語関数， https://reference.wolfram.com/language/ref/StructuralImportance.html.

CMS

Wolfram Language. 2012. "StructuralImportance." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/StructuralImportance.html.

APA

Wolfram Language. (2012). StructuralImportance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StructuralImportance.html

BibTeX

@misc{reference.wolfram_2024_structuralimportance, author="Wolfram Research", title="{StructuralImportance}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/StructuralImportance.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_structuralimportance, organization={Wolfram Research}, title={StructuralImportance}, year={2012}, url={https://reference.wolfram.com/language/ref/StructuralImportance.html}, note=[Accessed: 22-November-2024 ]}