SymmetricGroup

SymmetricGroup[n]

次数 n の対称群である．

詳細

  • SymmetricGroup[n]の次数 n は，非負の整数でなければならない．次数0および1は，自明群あるいは恒等群に対応する．
  • SymmetricGroup[n]はデフォルトで点{1,…,n}の置換群として表される．

予備知識

  • SymmetricGroup[n]は，対称群 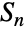（時に指定された非負の整数 n について，n 個のシンボル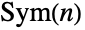として表される）を表す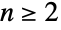．のとき，デフォルト表現のSymmetricGroup[n]はシンボルの置換群としてのものである．特殊ケースのSymmetricGroup[0]とSymmetricGroup[1]は厳密に1個の元を持つ自明群に等しい．
  • 数学的には，対称群 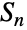（ただし 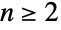）はシンボルの 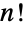回の置換と組成の群操作からなる．対称群は，したがって，位数 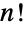の置換群であり，SymmetricGroup[n]の元はPermutations[Range[n]]と一致する．
  • 対称群は，抽象代数学，幾何学的群論，表現論，組合せ論，数理物理学において根本的な重要性を持つ．数多くの重要な数学的結果が対称群について成り立つ．例えば，ケイリー(Cayley)の定理には，すべての抽象群は対称群 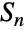のなんらかの部分群と同型である，とある．
  • SymmetricGroup[n]には，GroupOrder，GroupGenerators，GroupElements等を含む通常の群論関数を適用することができる．対称群 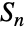の数多くの計算済み特性をFiniteGroupData[{"SymmetricGroup",n},"prop"]によって得ることができる．
  • SymmetricGroupは数多くの他のシンボルと関連がある．交代群と二面体群はどちらも対称群の重要な部分群である．Wolfram言語に組み込まれた，整数でパラメータ化される他の有限群の無限族には，AbelianGroup，AlternatingGroup，CyclicGroup，DihedralGroupがある．

例題

すべて開くすべて閉じる

例  (3)

対称群の元の数：

対称群の置換の生成元：

対称群の置換表現の元：

スコープ  (1)

次数が0または1である対称群は，自明群であり，単位元のみを含む：

その他の場合，次数 n の対称群は，n!個の要素を含む：

アプリケーション  (1)

2つのランダム置換が次数100の対称群を生成するかどうかを検証する：

特性と関係  (1)

Permutationsは，対称群の元の下に，式の置換された形式を返す：

Wolfram Research (2010), SymmetricGroup, Wolfram言語関数， https://reference.wolfram.com/language/ref/SymmetricGroup.html.

テキスト

Wolfram Research (2010), SymmetricGroup, Wolfram言語関数， https://reference.wolfram.com/language/ref/SymmetricGroup.html.

CMS

Wolfram Language. 2010. "SymmetricGroup." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SymmetricGroup.html.

APA

Wolfram Language. (2010). SymmetricGroup. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SymmetricGroup.html

BibTeX

@misc{reference.wolfram_2024_symmetricgroup, author="Wolfram Research", title="{SymmetricGroup}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/SymmetricGroup.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_symmetricgroup, organization={Wolfram Research}, title={SymmetricGroup}, year={2010}, url={https://reference.wolfram.com/language/ref/SymmetricGroup.html}, note=[Accessed: 18-November-2024 ]}