SymmetricGroup
代表一个次数为 n 的对称群.
背景
- SymmetricGroup[n] 表示对于给定非负整数 n 的 n 符号上的对称群
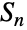 (有时表示为
(有时表示为 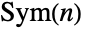 ). 对于
). 对于 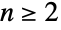 ,SymmetricGroup[n] 的默认表示是符号
,SymmetricGroup[n] 的默认表示是符号  上的置换群. 特殊情况 SymmetricGroup[0] 和 SymmetricGroup[1] 等同于只带一个元素的平凡群.
上的置换群. 特殊情况 SymmetricGroup[0] 和 SymmetricGroup[1] 等同于只带一个元素的平凡群. - 数学上,对称群
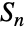 (对于
(对于 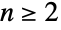 ) 组成符号
) 组成符号  的
的 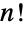 置换和群组合的运算. 对称群因此是阶数为
置换和群组合的运算. 对称群因此是阶数为 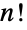 的置换群,SymmetricGroup[n] 的元素与 Permutations[Range[n]] 相重合.
的置换群,SymmetricGroup[n] 的元素与 Permutations[Range[n]] 相重合. - 对称群在抽象代数、几何群论、表示论、组合学和数学物理上至关重要. 对称群还有一些重要的数学结果. 例如,凯利(Cayley)理论阐明每个抽象群与对称群
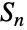 某些子群同构.
某些子群同构. - 一般的群理论函数可应用于 SymmetricGroup[n],包括 GroupOrder、GroupGenerators、GroupElements 等. 对称群
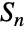 的预计算属性数值可通过 FiniteGroupData[{"SymmetricGroup",n},"prop"] 获取.
的预计算属性数值可通过 FiniteGroupData[{"SymmetricGroup",n},"prop"] 获取. - SymmetricGroup 也与其他符号相关. 交代群与二面体群是对称群的重要子群. 其他内置于 Wolfram 语言的被整数参数化的有限群的无限系列包括 AbelianGroup、AlternatingGroup、CyclicGroup 和 DihedralGroup.
范例
打开所有单元关闭所有单元属性和关系 (1)
Permutations 返回一个对称群元素作用下一个表达式的置换形式:
Wolfram Research (2010),SymmetricGroup,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SymmetricGroup.html.
文本
Wolfram Research (2010),SymmetricGroup,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SymmetricGroup.html.
CMS
Wolfram 语言. 2010. "SymmetricGroup." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SymmetricGroup.html.
APA
Wolfram 语言. (2010). SymmetricGroup. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SymmetricGroup.html 年