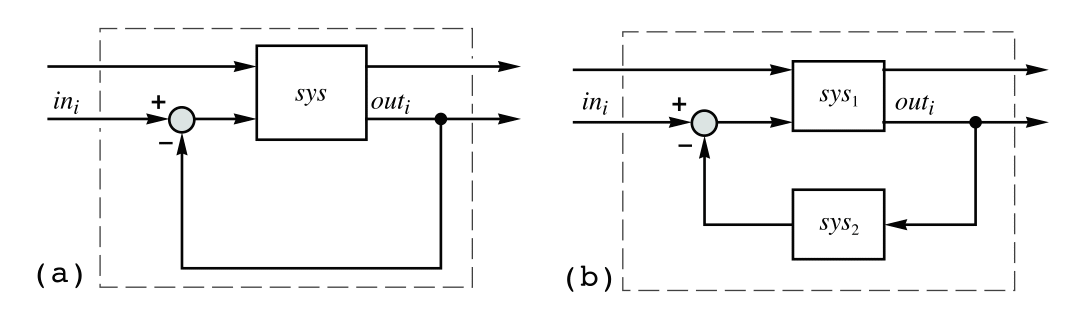
SystemsModelFeedbackConnect

SystemsModelFeedbackConnect[sys]

connects the outputs from sys to the inputs with negative feedback.

SystemsModelFeedbackConnect[sys,{con1,…}]

only feedback connect the outputs and inputs in coni.

SystemsModelFeedbackConnect[sys1,sys2]

connects the outputs of sys1 to sys2 and the outputs of sys2 to the inputs of sys1 in feedback.

SystemsModelFeedbackConnect[sys1,sys2,{out1,…},{{in1,ftype1},…}]

connects output outi of sys1 to the i^(th) input of sys2 and the j^(th) output of sys2 to input inj of sys1 with feedback type ftypej.

Details

  • The systems model sysi can be a TransferFunctionModel, StateSpaceModel, AffineStateSpaceModel, or NonlinearStateSpaceModel.
  • Connections coni can be given as:
  • {out,in}connect output out to input in in negative feedback
    {out,in,ftype}use positive or negative feedback type ftype
  • By default, sys2 is a unity gain system.
  • The arguments in, out, ini, and outi are integers specifying the positions of the input or output channels.
  • The ftype can be specified as "Negative" or -1 for negative feedback, and "Positive" or 1 for positive feedback. The default type is "Negative".

Examples

open allclose all

Basic Examples  (6)

A transfer function with negative unity feedback:

Connect two continuous-time systems in negative feedback:

Connect two discrete-time systems in negative feedback:

A state-space system with negative feedback:

Connect two state-space systems:

Feedback the second output to the first input:

Scope  (18)

Basic Uses  (10)

A unity negative feedback system:

A positive feedback system:

Connect two scalar systems:

Connect multivariable systems:

Connect the second output to the first input:

Connect the second output to the first input through a feedback system:

Connect discrete-time systems:

Connect two systems in positive feedback:

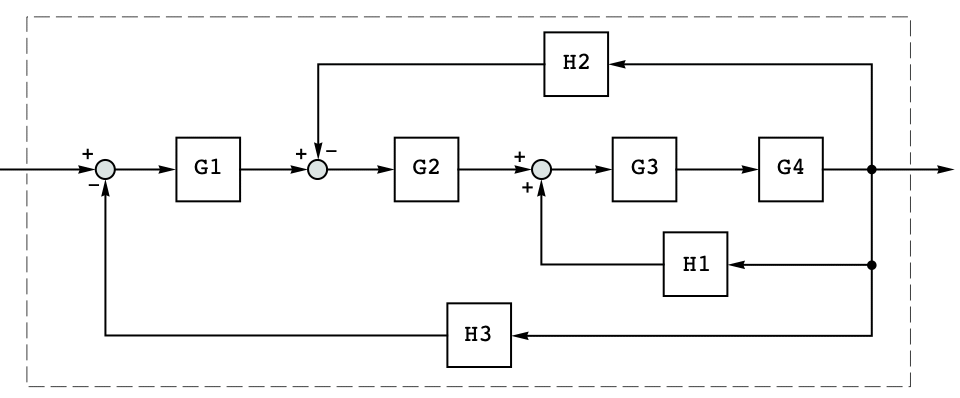
Connect two state-space models as shown in the diagram:

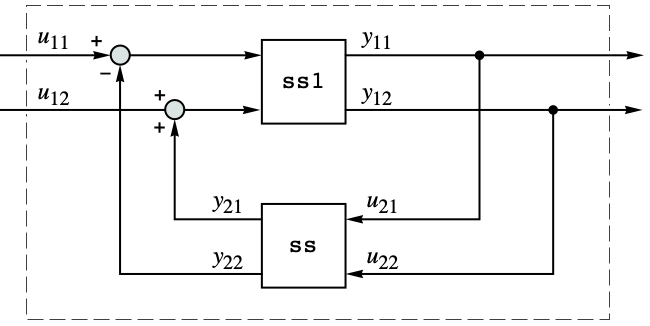
Connect a StateSpaceModel to a TransferFunctionModel:

System Types  (8)

Connect two TransferFunctionModel systems:

With delays:

Using improper transfer functions:

Connect two StateSpaceModel systems:

With delays:

Using descriptor state-space models:

Input linear AffineStateSpaceModel systems:

General nonlinear NonlinearStateSpaceModel systems:

Connecting a transfer function and state-space model will give a state-space model:

Connection with delays:

Connecting a standard linear system and an input linear system will give an affine model:

Connecting standard linear or affine system with a nonlinear system gives a nonlinear model:

Generalizations & Extensions  (2)

Use one feedback type for all connections:

Connect two systems with positive feedback:

Applications  (5)

Obtain the closed-loop transfer function of a discrete-time system with an integral controller and feedback sensor:

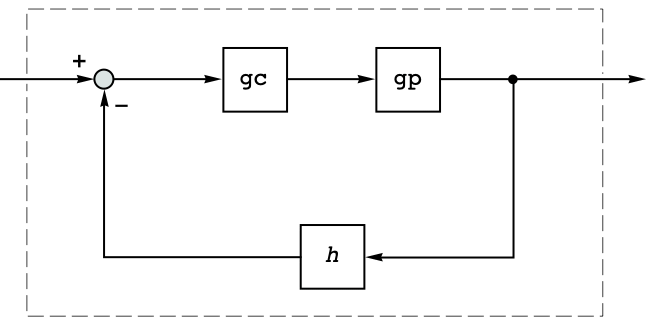
A motor-load servo system with position and velocity feedback:

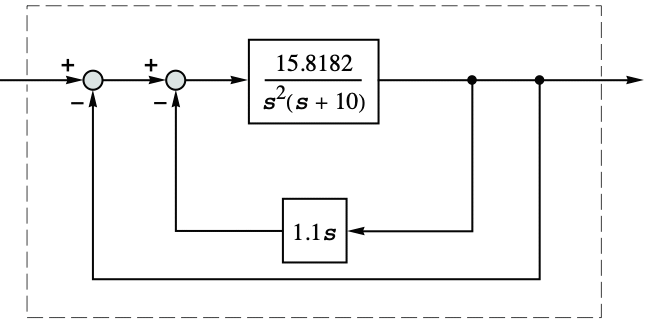
With only position feedback, the system is unstable:

The closed-loop system, with rate feedback in the inner loop and position feedback in the outer loop:

The response to a unit step:

Use SystemsModelFeedbackConnect in multi-loop reduction:

Compute the complementary sensitivity function from the loop transfer function:

A crankshaft receives a delayed input signal from the engine controller:

Including a simple controller shows the delay is internal to the closed-loop system:

Properties & Relations  (3)

The resulting system has the inputs and outputs of the first system:

SystemsModelFeedbackConnect is a special case of SystemsConnectionsModel:

Connect two transfer functions tfm1 and tfm2:

This is equivalent to (IdentityMatrix[n]+tfm1.tfm2)-1.tfm1:

Wolfram Research (2010), SystemsModelFeedbackConnect, Wolfram Language function, https://reference.wolfram.com/language/ref/SystemsModelFeedbackConnect.html (updated 2014).

Text

Wolfram Research (2010), SystemsModelFeedbackConnect, Wolfram Language function, https://reference.wolfram.com/language/ref/SystemsModelFeedbackConnect.html (updated 2014).

CMS

Wolfram Language. 2010. "SystemsModelFeedbackConnect." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/SystemsModelFeedbackConnect.html.

APA

Wolfram Language. (2010). SystemsModelFeedbackConnect. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SystemsModelFeedbackConnect.html

BibTeX

@misc{reference.wolfram_2025_systemsmodelfeedbackconnect, author="Wolfram Research", title="{SystemsModelFeedbackConnect}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/SystemsModelFeedbackConnect.html}", note=[Accessed: 24-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_systemsmodelfeedbackconnect, organization={Wolfram Research}, title={SystemsModelFeedbackConnect}, year={2014}, url={https://reference.wolfram.com/language/ref/SystemsModelFeedbackConnect.html}, note=[Accessed: 24-March-2025 ]}