WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

Tan[z]

z の正接を与える．

詳細
Details and Options Details and Options
予備知識
例題  
例  
スコープ  
数値評価  
特定の値  
可視化  
Show More Show More
関数の特性  
微分  
積分  
級数展開  
関数の恒等式と簡約  
関数表現  
アプリケーション  
特性と関係  
考えられる問題  
おもしろい例題  
関連項目
テクニカルノート
関連するガイド
関連リンク
履歴
引用書式

Tan

Tan[z]

z の正接を与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • Tanの引数はラジアンで与えられることを前提とする（Degreeで掛け合せることで度数から変換することができる）．
  • Sin[z]/Cos[z]はTan[z]へ自動的に変換される．TrigFactorList[expr]は分割を行う．
  • Tanは引数が 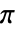の整数倍であるときは自動的に評価される．更に複雑な分数倍の場合，FunctionExpandを使う必要があることもある．
  • 特別な引数の場合，Tanは，自動的に厳密値を計算する．
  • Tanは任意の数値精度で評価できる．
  • Tanは自動的にリストに縫い込まれる． »
  • TanはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる． »

予備知識

  • Tanは，正接関数であり，これは三角法における基本関数の一つである．Tan[x]は，対応する正弦関数と余弦関数の比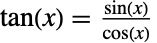として定義される．教科書的な定義では，直角三角形における角度 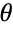の正接は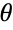， の向かい側の辺の長さと角の接する底辺の長さの比である．
  • Tanは，その引数が 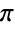の単純な有理倍数のときは，自動的に厳密値に評価される．より複雑な有理倍数については，FunctionExpandを使って明示的な厳密値を得ることができることがある．TrigFactorListを使ってTanを含む式を因数分解してSinとCosを含む項にすることができる．度で測られた角を使って引数を指定するときは，記号Degreeを乗数として使うことができる（例：Tan[30 Degree]）．引数として厳密な数式が与えられると，Tanは任意の数値精度に評価できることがある．Tanを含む記号式の操作に便利なその他の演算には，TrigToExp，TrigExpand，Simplify，FullSimplify等がある．
  • Tanは要素単位でリストおよび行列に縫い込まれる．個々の行列要素の正接とは対照的に，MatrixFunctionを使って，平方行列の正接（つまり，通常のベキが行列のベキで置き換えられた正接関数のベキ級数）を与えることができる．
  • Tanは，FunctionPeriodにあるように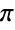， を周期として周期的である．Tanは，恒等式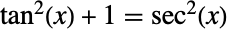を満足する．これは，ピタゴラス(Pythagorean)の定理に等しい．正接関数の定義は，定義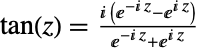を使って，複素数の引数 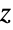にまで拡張される．ここで 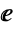は，自然対数の底である．Tanは，整数 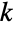について値 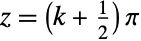で極を持ち，これらの点で ComplexInfinityに評価される．Tan[z]は，原点付近で級数展開sum_(k=0)^infty((-1)^(k-1) 2^(2 k)(2^(2k)-1) TemplateBox[{{2, , k}}, BernoulliB] )/((2 k)!)z^(2 k-1)を持つ．これはベルヌーイ(Bernoulli)数BernoulliBによって表すことができる．
  • Tanの逆関数は，ArcTanである．双曲線正接は，Tanhによって与えられる．他の関連する数学関数にはCot等がある．

例題

すべて開く すべて閉じる

例  (6)

引数はラジアンで与えられる：

Wolfram Language code: Tan[Pi / 6]

Degreeを用いて引数を度で指定する：

Wolfram Language code: Tan[30Degree]

実数の部分集合上でプロットする：

Wolfram Language code: Plot[Tan[x], {x, 0, 2Pi}]

複素数の部分集合上でプロットする：

Wolfram Language code: ComplexPlot3D[Tan[z], {z, -π - 2 I, π + 2 I}, PlotLegends -> Automatic, PlotRange -> {-2π, 2π}]

0における級数展開：

Wolfram Language code: Series[Tan[x], {x, 0, 10}]

特異点における漸近展開：

Wolfram Language code: Series[Tan[x], {x, π / 2, 5}]

スコープ  (46)

数値評価  (6)

数値的に評価する：

Wolfram Language code: Tan[1.2]

高精度で評価する：

Wolfram Language code: N[Tan[12 / 10], 50]

出力の精度は入力の精度に従う：

Wolfram Language code: Tan[1.20000000000000000000000]

Tanは複素数を入力として取る：

Wolfram Language code: Tan[2.5 + I]

Tanを高精度で効率よく評価する：

Wolfram Language code: Tan[1.2`500]//Timing
Wolfram Language code: Tan[1.2`100000];//Timing

自動縫込みを使って配列の要素ごとの値を計算する：

Wolfram Language code: Tan[ {{5π / 6, π}, {π / 3, -π}}]

MatrixFunctionを使って行列のTan関数を計算することもできる：

Wolfram Language code: MatrixFunction[Tan[#]&, {{5π / 6, π}, {π / 3, -π}}]

IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する：

Wolfram Language code: Tan[Interval[{0, π / 3}]]
Wolfram Language code: Tan[CenteredInterval[1, 1 / 100]]
Wolfram Language code: Tan[CenteredInterval[2 + 3I, (1 + I) / 100]]

Aroundを使って平均的な場合の統計区間を計算することもできる：

Wolfram Language code: Tan[Around[2, 0.02]]

特定の値  (5)

固定点におけるTanの値：

Wolfram Language code: Table[Tan[n (π/6)], {n, -2, 2}]

無限大における値：

Wolfram Language code: Tan[Infinity]
Wolfram Language code: Tan[ComplexInfinity]

Tanの零点：

Wolfram Language code: Assuming[m∈Integers, Refine[Tan[π m]]]

Solveを使って零点を1つ求める：

Wolfram Language code: sol = Solve[Tan[x] == 0 && -(π/2) < x < (π/2), x]

結果を代入する：

Wolfram Language code: xzero = x /. First[sol]

結果を可視化する：

Wolfram Language code: Plot[Tan[x], {x, -π / 2, π / 2}, Epilog -> Style[Point[{xzero, Tan[xzero]}], PointSize[Large], Red]]

Tanの特異点：

Wolfram Language code: Assuming[m∈Integers, FullSimplify[Refine[Tan[π ((1/2) + m)]]]]

簡単な厳密値は自動的に生成される：

Wolfram Language code: Tan[Pi / 5]

より複雑な場合はFunctionExpandを明示的に使う必要がある：

Wolfram Language code: Tan[Pi / 8]
Wolfram Language code: FunctionExpand[%]

可視化  (3)

Tan関数をプロットする：

Wolfram Language code: Plot[Tan[x], {x, -π, π}]

の実部をプロットする：

Wolfram Language code: ComplexContourPlot[Re[Tan[z]], {z, -π - I, π + I}, IconizedObject[«PlotOptions»]]

の虚部をプロットする：

Wolfram Language code: ComplexContourPlot[Im[Tan[z]], {z, -π - I, π + I}, IconizedObject[«PlotOptions»]]

の極プロット：

Wolfram Language code: Table[PolarPlot[Tan[k ϕ], {ϕ, -π, π}, Frame -> True, Exclusions -> All, FrameTicks -> {{{-1, -0.5, 0, 0.5, 1}, None}, {{-1, -0.5, 0, 0.5, 1}, None}}, PlotLabel -> "k=" <> ToString[k], PlotRange -> {{-1, 1}, {-1, 1}}], {k, 1, 4}]

関数の特性  (13)

Tanの実領域：

Wolfram Language code: FunctionDomain[Tan[x], x]

複素領域：

Wolfram Language code: FunctionDomain[Tan[z], z, Complexes]

Tanはすべての実数値に達する：

Wolfram Language code: FunctionRange[Tan[x], x, y]

Tanは周期 の周期関数である：

Wolfram Language code: FunctionPeriod[Tan[x], x]

Tanは奇関数である：

Wolfram Language code: Tan[-x]

Tanは鏡特性tan(TemplateBox[{z}, Conjugate])=TemplateBox[{{tan, (, z, )}}, Conjugate]を有する：

Wolfram Language code: FullSimplify[Tan[Conjugate[z]] == Conjugate[Tan[z]]]

Tanは解析関数ではない：

Wolfram Language code: FunctionAnalytic[Tan[x], x]

しかし，有理型である：

Wolfram Language code: FunctionMeromorphic[Tan[x], x]

Tanは特定の値域で単調である：

Wolfram Language code: FunctionMonotonicity[Tan[x], x]
Wolfram Language code: FunctionMonotonicity[{Tan[x], 0 < x < π / 2}, x]

Tanは単射ではない：

Wolfram Language code: FunctionInjective[Tan[x], x]
Wolfram Language code: Plot[{Tan[x], 1}, {x, -2π, 2π}]

Tanは全射である：

Wolfram Language code: FunctionSurjective[Tan[x], x]
Wolfram Language code: Plot[{Tan[x], 20}, {x, -2π, 2π}]

Tanは非負でも非正でもない：

Wolfram Language code: FunctionSign[Tan[x], x]

π/2の倍数の点に特異点と不連続点の両方を持つ：

Wolfram Language code: FunctionSingularities[Tan[x], x]
Wolfram Language code: FunctionDiscontinuities[Tan[x], x]

Tanは凸でも凹でもない：

Wolfram Language code: FunctionConvexity[Tan[x], x]

TraditionalFormによる表示：

Wolfram Language code: Tan[α]//TraditionalForm

微分  (3)

一次導関数：

Wolfram Language code: D[Tan[x], x]

高次導関数：

Wolfram Language code: Table[D[Tan[x], {x, n}], {n, 1, 3}]
Wolfram Language code: Plot[Evaluate[%], {x, -π, π}, PlotLegends -> {"First Derivative", "Second Derivative", "Third Derivative"}]

次導関数の式：

Wolfram Language code: D[Tan[x], {x, n}]
Wolfram Language code: Table[%, {n, 1, 3}]//Activate//Simplify

積分  (3)

Tanの不定積分：

Wolfram Language code: Integrate[Tan[x], x]

周期上のTanの定積分は0である：

Wolfram Language code: Integrate[Tan[x], {x, 0, π}, PrincipalValue -> True]

その他の積分例：

Wolfram Language code: Integrate[Tan[x]Cos[x], x]
Wolfram Language code: Integrate[Tan[z] ^ a, z]

級数展開  (3)

テイラー(Taylor)展開：

Wolfram Language code: Series[Tan[x], {x, 0, 7}]

の周りのTanの最初の3つの近似をプロットする：

Wolfram Language code: terms = Normal@Table[Series[Tan[x], {x, 0, m}], {m, 1, 5, 2}]; Plot[{Tan[x], terms}, {x, -(π/2), (π/2)}, PlotRange -> {{-(π/2), (π/2)}, Automatic}]

Tanの級数展開の一般項：

Wolfram Language code: SeriesCoefficient[Tan[x], {x, 0, n}]

Tanはベキ級数に適用できる：

Wolfram Language code: Tan[(π/2) + x + (x^2/2) + (x^3/3) + O[x]^4]

関数の恒等式と簡約  (6)

倍角のTan：

Wolfram Language code: Expand[Tan[2x] , Trig -> True]

総和のTan：

Wolfram Language code: Expand[Tan[x + y] , Trig -> True]

マルチアングルの式を変換する：

Wolfram Language code: TrigExpand[Tan[4x]]
Wolfram Language code: TrigReduce[%]

三角関数の総和を積に変換する：

Wolfram Language code: TrigFactor[Tan[x] + Tan[y]]

実変数 および を仮定して展開する：

Wolfram Language code: ComplexExpand[Tan[x + I y]]

複素指数に変換する：

Wolfram Language code: TrigToExp[Tan[z]]

関数表現  (4)

Cotを介して表現する：

Wolfram Language code: Simplify[Cot[(Pi/2) - x]]

ヤコビ関数を介した表現：

Wolfram Language code: Simplify[JacobiSC[z, 0]]
Wolfram Language code: Simplify[-I JacobiSN[I z, 1]]

SphericalHarmonicYを介した表現：

Wolfram Language code: Simplify[Sqrt[2]SphericalHarmonicY[1, -1, θ, 0] / SphericalHarmonicY[1, 0, θ, 0]]

マシュー(Mathieu)関数を介した表現：

Wolfram Language code: Simplify[(MathieuS[1, 0, z]/MathieuC[1, 0, z])]

アプリケーション  (4)

複素引数平面上にプロットを生成する：

Wolfram Language code: Plot3D[Re[Tan[x + I y]], {x, 0, 2Pi}, {y, 0, 3}]

移動する特異値を持つ微分方程式の解：

Wolfram Language code: DSolve[Derivative[1][w][z] - w[z]^2 - 1 == 0, w[z], z]

正接関数は等角的に放物線を単位円板にマップする：

Wolfram Language code: parabola = Table[1 - x ^ 2 / 4 + I x, {x, 0, 20, 1 / 10}];{Graphics[Point[{Re[#], Im[#]}]& /@ parabola, AspectRatio -> 1, Axes -> True], Graphics[Point[{Re[#], Im[#]}]& /@ (Tan[π / 4. Sqrt[parabola]] ^ 2), PlotRange -> All, Axes -> True]}

獲物が線に沿って2分の1の速さで移動している捕食動物の基準座標系内の追跡曲線：

Wolfram Language code: s = DSolve[{ℓ'[ϕ] == ℓ[ϕ] (Sin[ϕ] - 2) / Cos[ϕ], ℓ[0] == 1}, ℓ[ϕ], ϕ]//FullSimplify
Wolfram Language code: PolarPlot[Evaluate[ℓ[ϕ] /. s], {ϕ, 0, π / 2}, AspectRatio -> 1]

特性と関係  (13)

正接関数の基本的なパリティと周期性の性質は自動的に適用される：

Wolfram Language code: Tan[x + 2Pi]
Wolfram Language code: Tan[-x]
Wolfram Language code: Tan[I x]
Wolfram Language code: 1 / Tan[x]

TrigFactorListを用いてTanをSinとCosに因数分解する：

Wolfram Language code: Sin[x] / Cos[x]
Wolfram Language code: TrigFactorList[Tan[x]]

三角関数を含む複雑な式は自動的には簡約されない：

Wolfram Language code: Tan[z] + Cot[z]
Wolfram Language code: Simplify[%]

パラメータを仮定して簡約する：

Wolfram Language code: Tan[-x + k Pi]
Wolfram Language code: Simplify[%, k∈Integers]

逆関数を用いて構築する：

Wolfram Language code: {Tan[ArcTan[z]], Tan[2ArcTan[z]], Tan[3ArcTan[z]], Tan[4ArcTan[z]]}
Wolfram Language code: FunctionExpand[%]//Together

1ラジアンは度である：

Wolfram Language code: Tan[1] == TanDegrees[180 / π]//Simplify

三角方程式を解く：

Wolfram Language code: Reduce[Tan[z]^2 - 2 Tan[z + Pi / 4] == 4, z]

ゼロと極について解く：

Wolfram Language code: Reduce[Tan[α x + β] == 0, x]
Wolfram Language code: Reduce[1 / Tan[α x + β] == 0, x]

超越方程式の根を数値的に求める：

Wolfram Language code: FindRoot[Tan[z]^2 + 3 Tan[z + Pi / 6] + z == 4, {z, 2}]

積分：

Wolfram Language code: ∫Tan[z]^aⅆz

Tanは多くの数学関数の特殊形に現れる：

Wolfram Language code: {(MathieuS[1, 0, z]/MathieuC[1, 0, z]), JacobiSC[z, 0], JacobiCS[(π/2) - z, 0], JacobiSN[I z, 1], JacobiNS[(π I/2) - I z, 1], HypergeometricPFQ[{}, {(3/2)}, -z] / HypergeometricPFQ[{}, {(1/2)}, -z], MeijerG[{{}, {}}, {{(1/2)}, {0}}, z] / MeijerG[{{}, {}}, {{-(1/2)}, {0}}, z]}

剰余を記号的・数値的に計算する：

Wolfram Language code: Table[Residue[Tan[z]^k, {z, (π/2)}], {k, 5}]
Wolfram Language code: (1/2π I)NIntegrate[Tan[z], {z, (π/2) - (1/4), (π/2) - (I/4), (π/2) + (1/4), (π/2) + (I/4), (π/2) - (1/4)}]

Tanは数値関数である：

Wolfram Language code: Attributes[Tan]
Wolfram Language code: NumericQ[Tan[2 + E]]

考えられる問題  (4)

機械精度の入力では正解を出すのに不十分である：

Wolfram Language code: Tan[10. ^ 30]

厳密な入力を使うと，正しい答が得られる：

Wolfram Language code: N[Tan[10 ^ 30], 20]

$MaxExtraPrecisionの設定値を大きくする必要がある：

Wolfram Language code: N[Tan[10 ^ 100], 20]
Wolfram Language code: Block[{$MaxExtraPrecision = 200}, N[Tan[10 ^ 100], 20]]

出力精度は入力精度よりはるかに低くなることがある：

Wolfram Language code: Tan[1.5707963267948966192213216916397514421]

TraditionalFormでは引数の周りにカッコが必要である：

Wolfram Language code: tan x
Wolfram Language code: tan(x)

おもしろい例題  (7)

正接の積を計算する：

Wolfram Language code: Underoverscript[∏, k = 1, n - 1] Tan[z + (k π/n)]

正接の関数を積分する：

Wolfram Language code: Integrate[Tan[ArcCot[z]], z]

整数点でTanをプロットする：

Wolfram Language code: ArrayPlot[Table[ArcTan[Abs[Tan[x y]]], {x, -20, 20}, {y, -20, 20}]]

ネストした根基表現を与える：Give a nested radical representation:

Wolfram Language code: Tan[(π/2^12)]//FunctionExpand

連分数は極めて規則的である：

Wolfram Language code: ContinuedFraction[Tan[1], 22]

Cot[n]は，非零の整数 n における超越数である：

Wolfram Language code: Element[Tan[1], Algebraics]

正接の2D関数をプロットする：

Wolfram Language code: Plot3D[Tan[y ^ 2 - x ^ 3 + 3 x - 3], {x, -2, 2}, {y, -2, 2}, Exclusions -> {Cos[y ^ 2 - x ^ 3 + 3 x - 3] == 0}, PlotPoints -> 30, Mesh -> None]
Wolfram Research (1988), Tan, Wolfram言語関数， https://reference.wolfram.com/language/ref/Tan.html （2021年に更新）.

テキスト

Wolfram Research (1988), Tan, Wolfram言語関数， https://reference.wolfram.com/language/ref/Tan.html （2021年に更新）.

CMS

Wolfram Language. 1988. "Tan." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/Tan.html.

APA

Wolfram Language. (1988). Tan. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Tan.html

BibTeX

@misc{reference.wolfram_2026_tan, author="Wolfram Research", title="{Tan}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Tan.html}", note=[Accessed: 13-July-2026]}

BibLaTeX

@online{reference.wolfram_2026_tan, organization={Wolfram Research}, title={Tan}, year={2021}, url={https://reference.wolfram.com/language/ref/Tan.html}, note=[Accessed: 13-July-2026]}