TensorSymmetry

TensorSymmetry[tensor]

gives the symmetry of tensor under permutations of its slots.

TensorSymmetry[tensor,slots]

gives the symmetry under permutation of the specified list of slots.

Details and Options

  • TensorSymmetry accepts any type of tensor, either symbolic or explicit, including any type of array.
  • A general symmetry is specified by a generating set of pairs {perm,ϕ}, where perm is a permutation of the slots of the tensor, and ϕ is a root of unity. Each pair represents a symmetry of the tensor of the form ϕ TensorTranspose[tensor,perm]==tensor.
  • Some symmetry specifications have names:
  • Symmetric[{s1,…,sn}]full symmetry in the slots si
    Antisymmetric[{s1,…,sn}]antisymmetry in the slots si
    ZeroSymmetric[{s1,…,sn}]symmetry of a zero tensor
  • The following options can be given:
  • Assumptions$Assumptionsassumptions to make about tensors
    SameTestAutomaticfunction to test equality of expressions
    ToleranceAutomatictolerance for approximate numbers
  • For exact and symbolic arrays, the option SameTest->f indicates that two entries aij… and akl… are taken to be equal if f[aij…,akl…] gives True.
  • For approximate arrays, the option Tolerance->t can be used to indicate that all entries Abs[aij…]≤t are taken to be zero.
  • For array entries Abs[aij…]>t, equality comparison is done except for the last 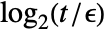bits, where 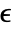is $MachineEpsilon for MachinePrecision arrays and 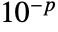for arrays of Precision .

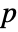Examples

open allclose all

Basic Examples  (2)

A symmetric matrix:

An antisymmetric matrix:

A symmetric array of rank 3:

Scope  (7)

Find symmetry in an array:

Find symmetries in complex arrays:

Symmetry of a SymmetrizedArray object:

Symmetry of a SparseArray object:

Specify the symmetry of a symbolic array:

Symmetry of its tensor product with itself. Note the exchange symmetry:

A fully symmetric rank 3 array:

Complete symmetry:

Symmetry in a subset of slots:

Symmetry of an array of zeros:

Options  (3)

Assumptions  (1)

Specify locally the properties of the tensors:

With no assumptions, the symmetry is unknown:

SameTest  (1)

This matrix is symmetric for a positive real , but TensorSymmetry gives no symmetry:

Use the option SameTest to get the correct answer:

Tolerance  (1)

Generate a fully symmetric random array of depth 4:

The addition of a small perturbation breaks the symmetry:

The symmetry can be recovered by allowing some tolerance:

Properties & Relations  (5)

Test whether a matrix is symmetric:

Find the symmetry of the matrix:

Test whether a matrix is antisymmetric:

Find the symmetry of the matrix:

Only a matrix of zeros can be simultaneously symmetric and antisymmetric:

Generation of special multidimensional symmetric arrays:

With a different radius, there are other symmetries:

The symmetry of Symmetrize[tensor,sym] is at least sym:

In some cases the result of Symmetrize[tensor,sym] may have more symmetry than sym:

Wolfram Research (2012), TensorSymmetry, Wolfram Language function, https://reference.wolfram.com/language/ref/TensorSymmetry.html (updated 2017).

Text

Wolfram Research (2012), TensorSymmetry, Wolfram Language function, https://reference.wolfram.com/language/ref/TensorSymmetry.html (updated 2017).

CMS

Wolfram Language. 2012. "TensorSymmetry." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/TensorSymmetry.html.

APA

Wolfram Language. (2012). TensorSymmetry. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TensorSymmetry.html

BibTeX

@misc{reference.wolfram_2024_tensorsymmetry, author="Wolfram Research", title="{TensorSymmetry}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/TensorSymmetry.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_tensorsymmetry, organization={Wolfram Research}, title={TensorSymmetry}, year={2017}, url={https://reference.wolfram.com/language/ref/TensorSymmetry.html}, note=[Accessed: 22-December-2024 ]}