TensorSymmetry

TensorSymmetry[tensor]

スロットの置換による tensor の対称を与える．

TensorSymmetry[tensor,slots]

指定されたスロットリストの置換の結果の対称を与える．

詳細とオプション

  • TensorSymmetryは，記号的であれ明示的であれ，任意のタイプの配列を含む，任意タイプのテンソルに使うことができる．
  • 一般的な対称性は生成元集合のペア{perm,ϕ}で指定される．ただし，perm はテンソルのスロットの置換で ϕ は1のベキ根である．各ペアはテンソルの対称性を ϕ TensorTranspose[tensor,perm]==tensor の形で表す．
  • 対称性の指定には名前のあるものがある．
  • Symmetric[{s1,…,sn}]スロット siで完全に対称
    Antisymmetric[{s1,…,sn}]スロット siで反対称
    ZeroSymmetric[{s1,…,sn}]ゼロテンソルの対称
  • 使用可能なオプション
  • Assumptions$Assumptionsテンソルについての仮定
    SameTestAutomatic式の等価性を検定する関数
    ToleranceAutomatic近似数の許容度
  • 厳密配列および記号配列については，オプションSameTest->f は f[aij…,akl…]がTrueを与えるならば2つの項目 aij…と akl…は等しいとみなされることを示す．
  • 近似配列については，オプションTolerance->t を使ってAbs[aij…]≤t であるすべての項目はゼロであるとみなされると示すことができる．
  • Abs[aij…]>t である配列の項目については，等価性の比較は最後の 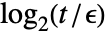ビットを除いて行われる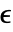． はMachinePrecision配列については$MachineEpsilonで，Precision 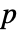の配列については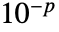である．

例題

すべて開くすべて閉じる

例  (2)

対称行列：

反対称行列：

階数3の対称配列：

スコープ  (7)

配列の中に対称性を求める：

複素配列の中に対称性を求める：

SymmetrizedArrayオブジェクトの対称性：

SparseArrayオブジェクトの対称性：

記号配列の対称性を指定する：

テンソル積のそれ自身との対称性．対称性の交換に注意のこと：

完全に対称な階数3の配列：

完全対称：

スロットの部分集合の対称：

ゼロ配列の対称：

オプション  (3)

Assumptions  (1)

テンソルの特性を局所的に指定する：

仮定がなければ対称性は未知である：

SameTest  (1)

次の行列は正の実数 については対称であるが，TensorSymmetryは非対称を与える：

オプションSameTestを使って正しい答を得る：

Tolerance  (1)

深さ4の完全に対称なランダム配列を生成する：

小さい摂動を加えると対称性が崩れる：

対称性は許容度を与えることで回復できる：

特性と関係  (5)

行列が対称かどうかを調べる：

行列の対称性を求める：

行列が非対称かどうかを調べる：

行列の対称性を求める：

零行列のみが同時に対称かつ非対称でありうる：

特別の多次元対称配列を生成する：

半径を変えると他の対称性が見付かる：

Symmetrize[tensor,sym]の対称性は，少なくとも sym である：

場合によっては，Symmetrize[tensor,sym]の結果の対称性が sym よりも高いことがある：

Wolfram Research (2012), TensorSymmetry, Wolfram言語関数， https://reference.wolfram.com/language/ref/TensorSymmetry.html （2017年に更新）.

テキスト

Wolfram Research (2012), TensorSymmetry, Wolfram言語関数， https://reference.wolfram.com/language/ref/TensorSymmetry.html （2017年に更新）.

CMS

Wolfram Language. 2012. "TensorSymmetry." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/TensorSymmetry.html.

APA

Wolfram Language. (2012). TensorSymmetry. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TensorSymmetry.html

BibTeX

@misc{reference.wolfram_2024_tensorsymmetry, author="Wolfram Research", title="{TensorSymmetry}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/TensorSymmetry.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_tensorsymmetry, organization={Wolfram Research}, title={TensorSymmetry}, year={2017}, url={https://reference.wolfram.com/language/ref/TensorSymmetry.html}, note=[Accessed: 22-November-2024 ]}