Torus[{x,y,z},{rinner,router}]
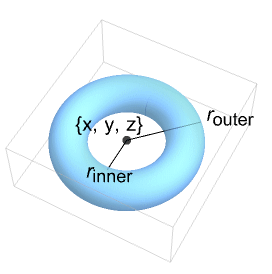
represents a torus centered at {x,y,z} with inner radius rinner and outer radius router.


Torus
Torus[{x,y,z},{rinner,router}]
represents a torus centered at {x,y,z} with inner radius rinner and outer radius router.
Details and Options

- Torus is also known as torus of revolution.
- Torus can be used as a geometric region and a 3D graphics primitive.
- Torus[] is equivalent to Torus[{0,0,0},{1/2,1}].
- Torus represents the shell
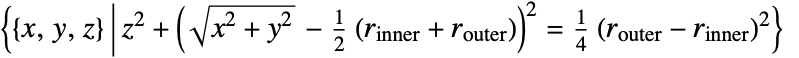 .
. - Torus can be used in Graphics3D.
- Graphics rendering is affected by directives such as FaceForm, Specularity, Opacity and color.
Examples
open all close allScope (18)
Graphics (9)
Applications (2)
Properties & Relations (3)
An implicit specification of a torus generated by ContourPlot3D:
A parametric specification of a torus generated by ParametricPlot3D:
Torus is the RegionBoundary of FilledTorus:
See Also
Related Guides
History
Text
Wolfram Research (2021), Torus, Wolfram Language function, https://reference.wolfram.com/language/ref/Torus.html.
CMS
Wolfram Language. 2021. "Torus." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Torus.html.
APA
Wolfram Language. (2021). Torus. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Torus.html
BibTeX
@misc{reference.wolfram_2025_torus, author="Wolfram Research", title="{Torus}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Torus.html}", note=[Accessed: 10-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_torus, organization={Wolfram Research}, title={Torus}, year={2021}, url={https://reference.wolfram.com/language/ref/Torus.html}, note=[Accessed: 10-March-2026]}