Cone

Cone[{{x1,y1,z1},{x2,y2,z2}},r]

represents a cone with a base of radius r centered at (x1,y1,z1) and a tip at (x2,y2,z2).

Cone[{{x1,y1,z1},{x2,y2,z2}}]

represents a cone with a base of radius 1.

Details and Options

  • Cone can be used as a geometric region and a graphics primitive.
  • Cone[] is equivalent to Cone[{{0,0,-1},{0,0,1}}].
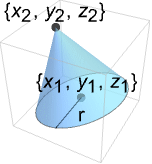
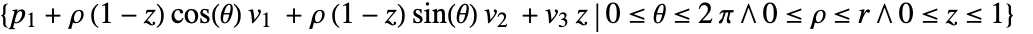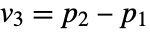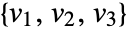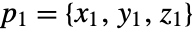  • Cone represents a filled cone region where and the vectors are orthogonal with TemplateBox[{{v, _, 1}}, Norm]=TemplateBox[{{v, _, 2}}, Norm]=1, and and .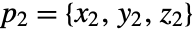
  • Cone can be used in Graphics3D.
  • In graphics, the points pi and radii r can be Scaled and Dynamic expressions.
  • Graphics rendering is affected by directives such as EdgeForm, FaceForm, Specularity, Opacity, and color.
  • Cone[{spec1,spec2,…},{r1,r2,…}] represents a collection of cones with specifications speci and base radii ri.

Examples

open allclose all

Basic Examples  (4)

A unit radius and two units height cone:

A cone from the origin to {1,1,1} with radius 1/2 at its base:

Differently styled cones:

Volume and centroid:

Scope  (22)

Graphics  (12)

Specification  (5)

If no radius is specified, it is assumed to be 1:

Cone with different radii:

Cone with different directions:

Short form for a cone centered at the origin with a base radius 1:

Multiple cones:

Styling  (5)

Color directives specify the face colors of cones:

FaceForm and EdgeForm can be used to specify the styles of the faces and edges:

Different properties can be specified for the front and back faces using FaceForm:

Cones with different specular exponents:

White cone that glows red:

Opacity specifies the face opacity:

Coordinates  (2)

Use Scaled coordinates:

Use Scaled radius:

Regions  (10)

Embedding dimension is the dimension of the space in which the cone lives:

Geometric dimension is the dimension of the shape itself:

Membership testing:

Get conditions for membership:

Volume:

Centroid:

Distance from a point:

The equidistance contours for a cone:

Signed distance from a point:

Nearest point in the region:

Nearest points to an enclosing sphere:

A cone is bounded:

Find its range:

Integrate over a cone region:

Optimize over a cone region:

Solve equations in a cone region:

Applications  (5)

Find the minimum surface area for a cone with volume :

Compare with some other cones of the same volume:

Define a region by the intersection of a cone and a plane:

Visualize the intersection:

A simple 3D arrow chart:

Define a ChartElementFunction based on Cone:

BarChart3D uses Cone to produce 3D bar charts:

Histogram3D can similarly use Cone:

Use Cone to display bubbles in BubbleChart3D:

Properties & Relations  (6)

Use Scale to get an elliptical cone:

Cone is used as a 3D arrowhead in Arrow:

Cone is a special case of Tube:

Get a truncated cone by specifying different radii in Tube:

A parametric specification of a cone shell generated using ParametricPlot3D:

An implicit specification of a cone shell generated by ContourPlot3D:

ImplicitRegion can represent any Cone region:

Neat Examples  (3)

Random unit cones:

Sweep a cone around an axis:

Nested transparent cones:

Wolfram Research (2008), Cone, Wolfram Language function, https://reference.wolfram.com/language/ref/Cone.html (updated 2014).

Text

Wolfram Research (2008), Cone, Wolfram Language function, https://reference.wolfram.com/language/ref/Cone.html (updated 2014).

CMS

Wolfram Language. 2008. "Cone." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/Cone.html.

APA

Wolfram Language. (2008). Cone. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Cone.html

BibTeX

@misc{reference.wolfram_2025_cone, author="Wolfram Research", title="{Cone}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Cone.html}", note=[Accessed: 22-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_cone, organization={Wolfram Research}, title={Cone}, year={2014}, url={https://reference.wolfram.com/language/ref/Cone.html}, note=[Accessed: 22-February-2025 ]}