Unequal 
lhs!=rhs or lhs≠rhs
returns False if lhs and rhs are identical.
Details
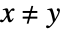can be entered as x∖[NotEqual]y or x 
!=
y. - lhs≠rhs returns True if lhs and rhs are determined to be unequal by comparisons between numbers or other raw data, such as strings.
- Approximate numbers are considered unequal if they differ beyond their last two decimal digits.
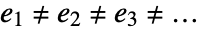gives True only if none of the ei are equal. 2≠3≠2->False. - lhs≠rhs represents a symbolic condition that can be generated and manipulated by functions like Reduce and LogicalExpand.
- Unequal[e] gives True.
- For exact numeric quantities, Unequal internally uses numerical approximations to establish inequality. This process can be affected by the setting of the global variable $MaxExtraPrecision.
- In StandardForm, Unequal is printed using ≠.
Background & Context
- Unequal[expr1,expr2] returns True if expr1 and expr2 are numerically unequal, False if they are equal and unevaluated if equality cannot be established. For example, Unequal[(1+Sqrt[5])/2,GoldenRatio] returns False, Unequal[1,2] returns True, and Unequal[1,a] returns unevaluated. Unequal[expr1,expr2] may be input as expr1!=expr2 or using the \[NotEqual] character as expr1≠expr2. The multiple-argument form Unequal[expr1,expr2,…], which may also be input as expr1!=expr2!=…, returns True if none of the expressions expri are numerically equal, False if any two are equal and unevaluated otherwise. The single-argument form Unequal[expr] returns True (as, slightly paradoxically, does the single-argument form Equal[expr]).
- Numbers with machine precision (MachinePrecision) or greater are considered equal if they differ in at most their last seven binary digits and unequal otherwise. Equality for numbers below machine precision is established based on agreement to within the precision of the lowest precision number. For example, 1.01`2!=1 returns False, while 1.01`3==1 returns True. For exact numeric quantities, Unequal uses numerical approximations to establish inequality, which can be affected by the value of the global variable $MaxExtraPrecision.
- Unequal is related to a number of other symbols. UnsameQ[expr1,expr2] (which may be input as expr1=!=expr2) returns True if expr1 and expr2 differ in their underlying FullForm representations and otherwise returns False. In contrast to Unequal, UnsameQ differentiates between different representations of numbers; for example, UnsameQ[1,1.] and UnsameQ[1.,1.+0.I] both return True. The behavior of UnsameQ also differs from that of Unequal in that UnsameQ always evaluates to True or False, whereas Unequal may remain unevaluated in cases where equality cannot be resolved. Equal (which may be input as expr1==expr2) is the converse of Unequal. Unequal also has an operator form UnequalTo.
- PossibleZeroQ can be used to indicate if a given expression has value
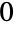in some cases where Unequal returns unevaluated. For example, Unequal[Erf[Log[4]+2Log[Sin[Pi/8]]]-Erf[Log[2-Sqrt[2]]],0] returns evaluated, while calling PossibleZeroQ on its first argument returns True (together with an informative message indicating that a zero value could not be rigorously established). Symbolic simplifiers like Simplify, FullSimplify and RootReduce can sometimes also be used to rigorously establish equality (including in the example just given) when Unequal cannot.
Examples
open allclose allBasic Examples (2)
Returns True if elements are guaranteed unequal, and otherwise stays unevaluated:
:Scope (11)
Numeric Inequations (6)
Approximate numbers that differ in at most their last eight binary digits are considered equal:
Compare an exact numeric expression and an approximate number:
Compare two exact numeric expressions; a numeric test may suffice to prove unequality:
Proving equality requires symbolic methods:
Symbolic methods used by Unequal are insufficient to prove this False:
Use RootReduce to decide whether two algebraic numbers are unequal:
Numeric methods used by Unequal do not use sufficient precision to prove this unequality:
RootReduce proves that the two algebraic numbers are not equal:
Increasing $MaxExtraPrecision may also prove unequality:
Properties & Relations (4)
The negation of two-argument Unequal is Equal:
The negation of three-argument Unequal does not simplify automatically:
Use LogicalExpand to express it in terms of two-argument Equal:
The negation of three-argument Unequal is not equivalent to three-argument Equal:
Unequal tests mathematical unequality of objects represented by expressions:
UnsameQ tests syntactic unequality of expressions:
When Unequal cannot decide whether two numeric expressions are equal it returns unchanged:
FullSimplify uses exact symbolic transformations to disprove the unequality:
PossibleZeroQ uses numeric and symbolic heuristics to decide whether an expression is zero:
Numeric methods used by PossibleZeroQ may incorrectly decide that a number is zero:
Possible Issues (3)
Unequality for machine-precision approximate numbers can be subtle:
The extra digits disrupt equality:
Arbitrary-precision approximate numbers do not have this problem:
Thanks to automatic-precision tracking, Unequal knows to look only at the first 10 digits:
In this case, the unequality test for machine numbers gives the expected result:
The extra digits in this case are ignored by Unequal:
Text
Wolfram Research (1988), Unequal, Wolfram Language function, https://reference.wolfram.com/language/ref/Unequal.html (updated 1996).
CMS
Wolfram Language. 1988. "Unequal." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/Unequal.html.
APA
Wolfram Language. (1988). Unequal. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Unequal.html