xy or VectorGreater[{x,y}]
yields True for vectors of length n if xi>yi for all components ![]() .
.
xκy or VectorGreater[{x,y},κ]
yields True for x and y if ![]() , where κ is a proper convex cone.
, where κ is a proper convex cone.


VectorGreater 
xy or VectorGreater[{x,y}]
yields True for vectors of length n if xi>yi for all components ![]() .
.
xκy or VectorGreater[{x,y},κ]
yields True for x and y if ![]() , where κ is a proper convex cone.
, where κ is a proper convex cone.
Details


- VectorGreater gives a partial ordering of vectors, matrices and arrays that is compatible with vector space operations, so that
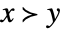 and
and 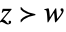 imply
imply 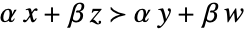 for all
for all 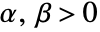 .
. - VectorGreater is typically used to specify vector inequalities for constrained optimization, inequality solving and integration.
- When x and y are
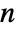 -vectors, xy is equivalent to
-vectors, xy is equivalent to  . That is, each part of x is greater than the corresponding part of y for the relation to be true.
. That is, each part of x is greater than the corresponding part of y for the relation to be true. - When x and y are dimension
 arrays, xy is equivalent to
arrays, xy is equivalent to 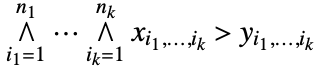 . That is, each part of x is greater than the corresponding part of y for the relation to be true.
. That is, each part of x is greater than the corresponding part of y for the relation to be true. - xy remains unevaluated if x or y has non-numeric elements; typically gives True or False otherwise.
- When x is an n-vector and y is a numeric scalar, xy yields True if xi>y for all components
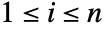 .
. - By using the character , entered as
 v>
v> or \[VectorGreater], with subscripts vector inequalities can be entered as follows:
or \[VectorGreater], with subscripts vector inequalities can be entered as follows: -
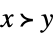
VectorGreater[{x,y}] the standard vector inequality 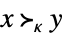
VectorGreater[{x,y},κ] vector inequality defined by a cone κ - In general, one can use a proper convex cone κ to specify a vector inequality. The set
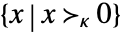 is the same as κ.
is the same as κ. - Possible cone specifications κ in
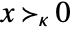 for vectors x include:
for vectors x include: -
{"NonNegativeCone", n} ![TemplateBox[{n}, NonNegativeConeList] TemplateBox[{n}, NonNegativeConeList]](Files/VectorGreater.en/22.png)
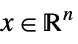 such that
such that 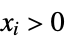
{"NormCone", n} ![TemplateBox[{n}, NormConeList] TemplateBox[{n}, NormConeList]](Files/VectorGreater.en/25.png)
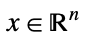 such that Norm[{x1,…,xn-1}]<xn
such that Norm[{x1,…,xn-1}]<xn"ExponentialCone" ![TemplateBox[{}, ExponentialConeString] TemplateBox[{}, ExponentialConeString]](Files/VectorGreater.en/27.png)
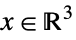 such that
such that 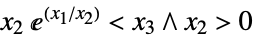
"DualExponentialCone" ![TemplateBox[{}, DualExponentialConeString] TemplateBox[{}, DualExponentialConeString]](Files/VectorGreater.en/30.png)
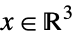 such that
such that 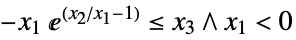
{"PowerCone",α} ![TemplateBox[{alpha}, PowerConeList] TemplateBox[{alpha}, PowerConeList]](Files/VectorGreater.en/33.png)
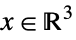 such that
such that 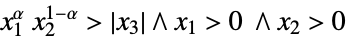
{"DualPowerCone",α} ![TemplateBox[{alpha}, DualPowerConeList] TemplateBox[{alpha}, DualPowerConeList]](Files/VectorGreater.en/36.png)
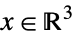 such that
such that 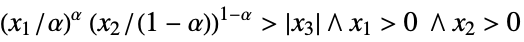
- Possible cone specifications κ in
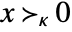 for matrices x include:
for matrices x include: -
"NonNegativeCone" ![TemplateBox[{}, NonNegativeConeString] TemplateBox[{}, NonNegativeConeString]](Files/VectorGreater.en/40.png)
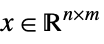 such that
such that 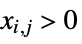
{"SemidefiniteCone", n} ![TemplateBox[{n}, SemidefiniteConeList] TemplateBox[{n}, SemidefiniteConeList]](Files/VectorGreater.en/43.png)
symmetric positive definite matrices 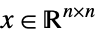
- Possible cone specifications κ in
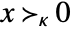 for arrays x include:
for arrays x include: -
"NonNegativeCone" ![TemplateBox[{}, NonNegativeConeString] TemplateBox[{}, NonNegativeConeString]](Files/VectorGreater.en/46.png)
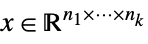 such that
such that 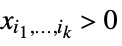
- For exact numeric quantities, VectorGreater internally uses numerical approximations to establish numerical ordering. This process can be affected by the setting of the global variable $MaxExtraPrecision.
Examples
open all close allBasic Examples (3)
Scope (7)
Determine if all of the elements in a vector are non-negative:
Determine if all components are less than or equal to 1:
For each component, !xi≥yi does imply xi<yi:
Compare the components of two matrices:
Represent the condition that Norm[{x,y}]<=1:
Represent the condition that ![]() :
:
Show the boundary of where ![]() for non-negative x,y with α between 0 and 1:
for non-negative x,y with α between 0 and 1:
Applications (1)
VectorGreater is a fast way to compare many elements:
Properties & Relations (3)
VectorGreater is compatible with a vector space operation:
Adding vectors to both sides of ![]() for any vector
for any vector ![]() :
:
Multiplying by positive constants ![]() for any
for any ![]() :
:
xκy are (strict) partial orders, i.e. irreflexive, asymmetric and transitive:
Irreflexive, i.e. ![]() for all elements
for all elements ![]() so no element is related to itself:
so no element is related to itself:
Transitive, i.e. if ![]() and
and ![]() then
then ![]() :
:
xκy are partial orders but not total orders, so there are incomparable elements:
Neither ![]() nor
nor ![]() is true, because
is true, because ![]() and
and ![]() are incomparable elements:
are incomparable elements:
The set of vectors ![]() and
and ![]() . These are the only comparable elements to
. These are the only comparable elements to ![]() :
:
Related Guides
History
Text
Wolfram Research (2019), VectorGreater, Wolfram Language function, https://reference.wolfram.com/language/ref/VectorGreater.html.
CMS
Wolfram Language. 2019. "VectorGreater." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/VectorGreater.html.
APA
Wolfram Language. (2019). VectorGreater. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VectorGreater.html
BibTeX
@misc{reference.wolfram_2025_vectorgreater, author="Wolfram Research", title="{VectorGreater}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/VectorGreater.html}", note=[Accessed: 25-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_vectorgreater, organization={Wolfram Research}, title={VectorGreater}, year={2019}, url={https://reference.wolfram.com/language/ref/VectorGreater.html}, note=[Accessed: 25-February-2026]}