VoronoiMesh

VoronoiMesh[{p1,…,pn}]

gives a MeshRegion representing the Voronoi mesh from the points p1, p2, ….

VoronoiMesh[{p1,…,pn},{{xmin,xmax},…}]

clips the mesh to the bounds .

Details and Options

  • VoronoiMesh is also known as Voronoi diagram and Dirichlet tessellation.
  • The Voronoi mesh consists of n convex cells, each associated with a point pi and defined by 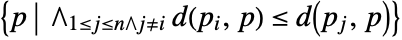, which is the region of points closer to pi than any other point pj for j≠i.
  • The cells associated with the outer points will be unbounded, but only a bounded range will be returned. If no explicit range {{xmin,xmax},…} is given, a range is computed automatically.
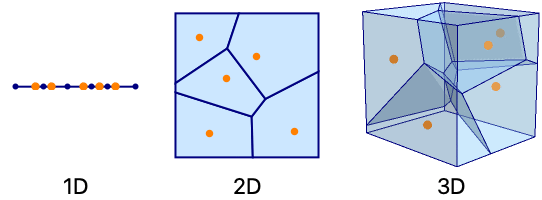
  • The cells will be intervals in 1D, convex polygons in 2D and convex polyhedra in 3D.
  • VoronoiMesh takes the same options as MeshRegion.

Examples

open allclose all

Basic Examples  (2)

Create a 1D Voronoi mesh from a set of points:

Each point corresponds to a Voronoi cell, which is an interval in the 1D case:

Create a 2D Voronoi mesh from a set of points:

Each point corresponds to a Voronoi cell:

Scope  (2)

Create a 1D Voronoi mesh from a set of points:

Basic properties:

Voronoi meshes are full-dimensional:

Voronoi meshes are bounded by their clipping values:

Create a 2D Voronoi mesh from a set of points:

Basic properties:

Voronoi meshes are full-dimensional:

Voronoi meshes are bounded by their clipping values:

Options  (11)

MeshCellHighlight  (2)

MeshCellHighlight allows you to specify highlighting for parts of a VoronoiMesh:

Individual cells can be highlighted using their cell index:

Or by the cell itself:

MeshCellLabel  (2)

MeshCellLabel can be used to label parts of a VoronoiMesh:

Individual cells can be labeled using their cell index:

Or by the cell itself:

MeshCellMarker  (1)

MeshCellMarker can be used to assign values to parts of a VoronoiMesh:

Use MeshCellLabel to show the markers:

MeshCellShapeFunction  (2)

MeshCellShapeFunction allows you to specify functions for parts of a VoronoiMesh:

Individual cells can be drawn using their cell index:

Or by the cell itself:

MeshCellStyle  (2)

MeshCellStyle allows you to specify styling for parts of a VoronoiMesh:

Individual cells can be highlighted using their cell index:

Or by the cell itself:

PlotTheme  (2)

Use a theme with grid lines and a legend:

Use a theme to draw a wireframe:

Applications  (8)

Basic Applications  (2)

Create an interactive Voronoi mesh with draggable points. Use Click on the Voronoi mesh to add and remove draggable points:

Voronoi meshes for simple point configurations including a grid:

A circle of points:

Geography  (1)

Create an interactive map of the closest large city in Italy. Start by getting names and coordinate data for large cities in Italy:

Nearest function for labeling region cells:

Generate a Voronoi mesh from city coordinates:

Create a tooltip map from the Voronoi mesh:

Mouse over the map to get the name of the closest large city:

Physics  (1)

Given a 2D lattice basis:

Generate lattice points:

Generate and visualize the Voronoi cells, also known as Brillouin zones:

Image Processing  (1)

Create a polygonal mosaic from an image:

Find the edges of the image:

Create a Voronoi mesh from the edge positions:

Recursively apply VoronoiMesh to the mean vertex positions of the precursive Voronoi cells to create a more uniform mesh:

Color each polygon with the image color coinciding with its mean vertex positions:

Other  (3)

Create a jigsaw puzzle from a random Voronoi mesh:

Extract lines from the mesh:

Define a function that converts a line to an interlocking edge:

Replace lines of sufficient length with an interlocking edge:

Visualize the result:

Visualize a piecewise constant interpolation of a function over a set of random point samples:

Voronoi mesh from , sample coordinates:

Function to rescale values to :

Piecewise constant contour plot of sample data:

A similar plot can also be achieved with ListContourPlot:

Plan a path for a point robot through a random set of point obstacles by following Voronoi edges:

Generate Voronoi edges around the obstacles:

Create an undirected Graph from the Voronoi edges with their lengths as edge weights:

Use Nearest function to find the closest Voronoi vertices to the start and end points:

Drag starting or ending points to explore different paths (red):

Properties & Relations  (5)

The output of VoronoiMesh is always a full-dimensional MeshRegion:

Each point of the original data is contained in exactly one cell in the Voronoi mesh:

VoronoiMesh is the dual of the DelaunayMesh:

Each Voronoi cell has a single point from the original point set:

The Voronoi cell for pi is given by :

Generate the conditions for each cell:

DistanceTransform for black points on a white background will be similar to VoronoiMesh:

Wolfram Research (2014), VoronoiMesh, Wolfram Language function, https://reference.wolfram.com/language/ref/VoronoiMesh.html (updated 2022).

Text

Wolfram Research (2014), VoronoiMesh, Wolfram Language function, https://reference.wolfram.com/language/ref/VoronoiMesh.html (updated 2022).

CMS

Wolfram Language. 2014. "VoronoiMesh." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/VoronoiMesh.html.

APA

Wolfram Language. (2014). VoronoiMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VoronoiMesh.html

BibTeX

@misc{reference.wolfram_2024_voronoimesh, author="Wolfram Research", title="{VoronoiMesh}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/VoronoiMesh.html}", note=[Accessed: 30-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_voronoimesh, organization={Wolfram Research}, title={VoronoiMesh}, year={2022}, url={https://reference.wolfram.com/language/ref/VoronoiMesh.html}, note=[Accessed: 30-December-2024 ]}