WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

WeightedAdjacencyMatrix

WeightedAdjacencyMatrix[g]

グラフ g の辺の重みがある隣接行列を与える．

WeightedAdjacencyMatrix[{vw,…}]

規則 vw を使ってグラフ g を指定する．

詳細とオプション

WeightedAdjacencyMatrixはSparseArrayオブジェクトを返す．これはNormalを使って通常の行列に変換することができる．
重み付き隣接行列の項 w_ijは頂点 ν_iから頂点 ν_jへの有向辺の重みである．そこに辺がなければ重みは0であるとみなされる．
明示的にEdgeWeightが指定されていない辺の重みは1であるとみなされる．
1本の無向辺は方向が逆で重みが等しい2本の有向辺であるとみなされる．
頂点 v_iはVertexList[g]で与えられる順序であるとみなされる．
グラフの重み付き隣接行列の次元は 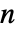× 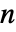である．ただし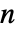，は頂点数である．

例題

すべて開くすべて閉じる

例 (2)

無向グラフの重み付き隣接行列：

有向グラフの重み付き隣接行列：

スコープ (5)

無向グラフの重み付き隣接行列は対称である：

有向グラフの重み付き隣接行列は対称ではないことがある：

規則を使ってグラフを指定する：

自己ループがあるグラフの重み付き隣接行列には対角項目がある：

WeightedAdjacencyMatrixは大きいグラフに使える：

MatrixPlotを使って行列を可視化する：

特性と関係 (4)

重み付き隣接行列の行と列はVertexListで与えられる順に従う：

WeightedAdjacencyGraphを使って重み付き隣接行列からグラフを構築する：

行数と列数は頂点数と同じである：

ループのないグラフの主対角項はすべて0である：

トップへ