WeightedAdjacencyMatrix

WeightedAdjacencyMatrix[g]

给出图 g 的带有边的权值的邻接矩阵.

WeightedAdjacencyMatrix[{vw,…}]

使用规则 vw 来指定图 g.

更多信息和选项

  • WeightedAdjacencyMatrix 返回一个 SparseArray 对象，该对象可以使用 Normal 转化为一个普通矩阵.
  • 加权邻接矩阵的元素 wij 是从顶点 νi 到顶点 νj 的有向边的权值. 如果不存在边，则权值为0.
  • 如果一条边的 EdgeWeight 没有显式指定，则权值取1.
  • 一个无向边解释为具有相反方向和相同权值的两条有向边.
  • 认为顶点 vi 遵循由 VertexList[g] 给出的顺序.
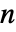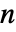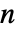  • 一个图的加权邻接矩阵具有维度 ×，其中 是顶点数.

范例

打开所有单元关闭所有单元

基本范例  (2)

一个无向图的加权邻接矩阵：

一个有向图的加权邻接矩阵：

范围  (5)

无向图的加权邻接矩阵是对称的：

有向图的加权邻接矩阵可以是非对称的：

使用规则来指定图：

具有自环的图的加权邻接矩阵有对角元素：

WeightedAdjacencyMatrix 对大规模图起作用：

使用 MatrixPlot 作出矩阵的视图：

属性和关系  (4)

加权邻接矩阵的行和列遵循由 VertexList 给出的顺序：

使用 WeightedAdjacencyGraph 来从加权邻接矩阵构建一个图：

行数或者列数等于顶点数：

无环图的主对角线都是零：

Wolfram Research (2010)，WeightedAdjacencyMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/WeightedAdjacencyMatrix.html （更新于 2015 年）.

文本

Wolfram Research (2010)，WeightedAdjacencyMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/WeightedAdjacencyMatrix.html （更新于 2015 年）.

CMS

Wolfram 语言. 2010. "WeightedAdjacencyMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/WeightedAdjacencyMatrix.html.

APA

Wolfram 语言. (2010). WeightedAdjacencyMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/WeightedAdjacencyMatrix.html 年

BibTeX

@misc{reference.wolfram_2024_weightedadjacencymatrix, author="Wolfram Research", title="{WeightedAdjacencyMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/WeightedAdjacencyMatrix.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_weightedadjacencymatrix, organization={Wolfram Research}, title={WeightedAdjacencyMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/WeightedAdjacencyMatrix.html}, note=[Accessed: 22-November-2024 ]}