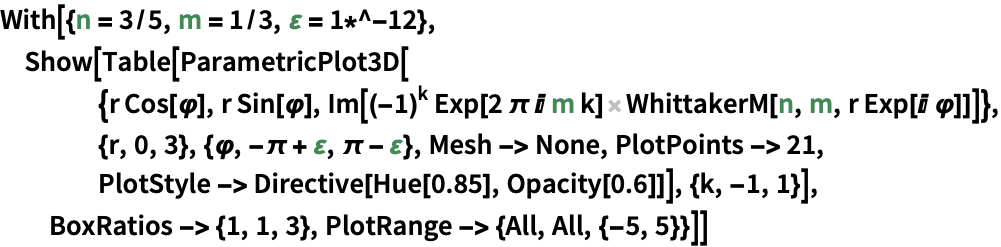WhittakerM
✖
WhittakerM
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
- WhittakerM is related to the Kummer confluent hypergeometric function by
![TemplateBox[{k, m, z}, WhittakerM]=e^(-z/2)z^(m+1/2) TemplateBox[{{m, -, k, +, {1, /, 2}}, {{2, , m}, +, 1}, z}, Hypergeometric1F1] TemplateBox[{k, m, z}, WhittakerM]=e^(-z/2)z^(m+1/2) TemplateBox[{{m, -, k, +, {1, /, 2}}, {{2, , m}, +, 1}, z}, Hypergeometric1F1]](Files/WhittakerM.en/2.png) .
. ![TemplateBox[{k, m, z}, WhittakerM] TemplateBox[{k, m, z}, WhittakerM]](Files/WhittakerM.en/3.png) vanishes at
vanishes at 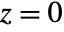 for
for 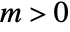 .
. - For certain special arguments, WhittakerM automatically evaluates to exact values.
- WhittakerM can be evaluated to arbitrary numerical precision.
- WhittakerM automatically threads over lists.
- WhittakerM[k,m,z] has a branch cut discontinuity in the complex
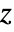 plane running from
plane running from 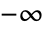 to
to 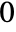 .
. - WhittakerM can be used with Interval and CenteredInterval objects. »
Examples
open allclose allBasic Examples (6)Summary of the most common use cases
https://wolfram.com/xid/0j49rir4-nkyuf
Use FunctionExpand to expand in terms of hypergeometric functions:
https://wolfram.com/xid/0j49rir4-5fexz
Plot over a subset of the reals ![]() :
:
https://wolfram.com/xid/0j49rir4-fknucq
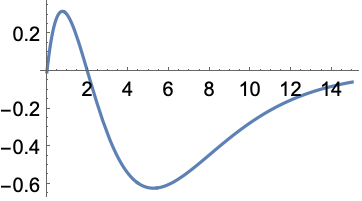
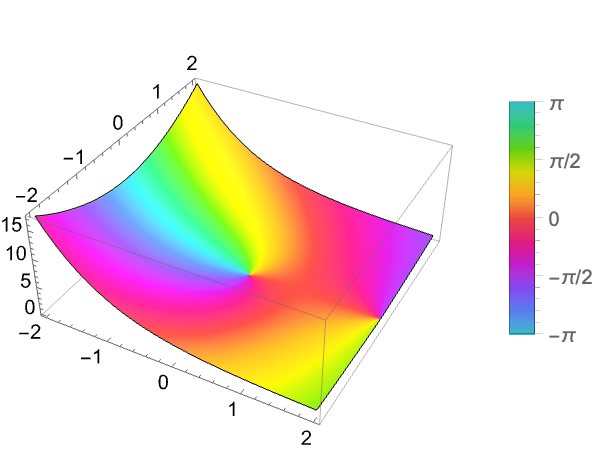
Plot over a subset of the complexes:
https://wolfram.com/xid/0j49rir4-kiedlx
Series expansion at the origin:
https://wolfram.com/xid/0j49rir4-t1nfp
Series expansion at Infinity:
https://wolfram.com/xid/0j49rir4-cugjvu
Scope (35)Survey of the scope of standard use cases
Numerical Evaluation (6)
https://wolfram.com/xid/0j49rir4-l274ju
https://wolfram.com/xid/0j49rir4-cksbl4
https://wolfram.com/xid/0j49rir4-b0wt9
The precision of the output tracks the precision of the input:
https://wolfram.com/xid/0j49rir4-y7k4a
https://wolfram.com/xid/0j49rir4-hfml09
Evaluate efficiently at high precision:
https://wolfram.com/xid/0j49rir4-di5gcr

https://wolfram.com/xid/0j49rir4-bq2c6r
WhittakerM can be used with Interval and CenteredInterval objects:
https://wolfram.com/xid/0j49rir4-h0d6g
https://wolfram.com/xid/0j49rir4-dj6d9x
Compute the elementwise values of an array:
https://wolfram.com/xid/0j49rir4-thgd2
Or compute the matrix WhittakerM function using MatrixFunction:
https://wolfram.com/xid/0j49rir4-o5jpo
Specific Values (7)
WhittakerM for symbolic parameters:
https://wolfram.com/xid/0j49rir4-fc9m8o
https://wolfram.com/xid/0j49rir4-bmqd0y
https://wolfram.com/xid/0j49rir4-e41pf2
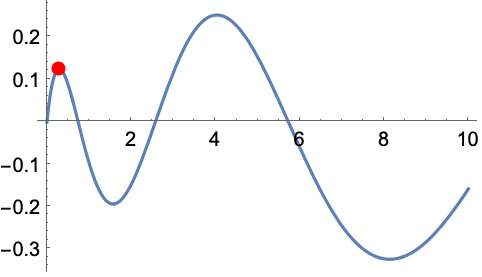
Find the first positive maximum of WhittakerM[5,1/2,x]:
https://wolfram.com/xid/0j49rir4-f2hrld
https://wolfram.com/xid/0j49rir4-fkkzx
Compute the associated WhittakerM[3,1/2,x] function:
https://wolfram.com/xid/0j49rir4-klij8s
Compute the associated WhittakerM function for half-integer parameters:
https://wolfram.com/xid/0j49rir4-hfz8z6
Different cases of WhittakerM give different symbolic forms:
https://wolfram.com/xid/0j49rir4-chhice
WhittakerM threads elementwise over lists:
https://wolfram.com/xid/0j49rir4-m2hznn
Visualization (3)
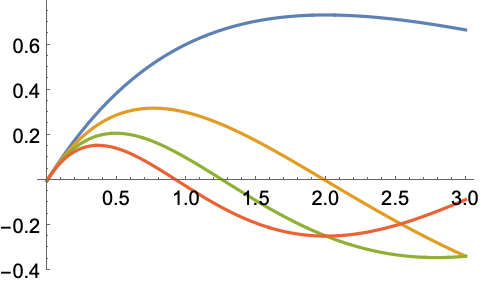
Plot the WhittakerM function for various orders:
https://wolfram.com/xid/0j49rir4-ecj8m7
https://wolfram.com/xid/0j49rir4-zpq38
https://wolfram.com/xid/0j49rir4-f87e
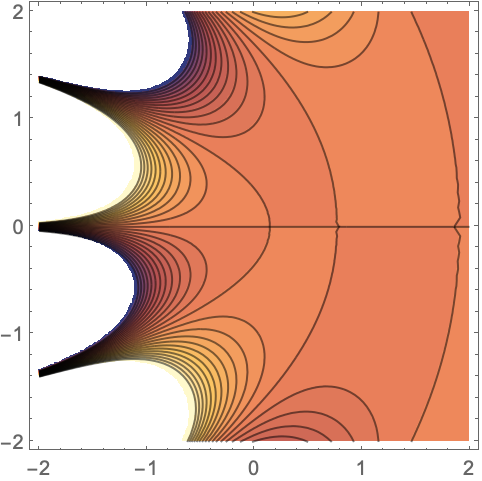
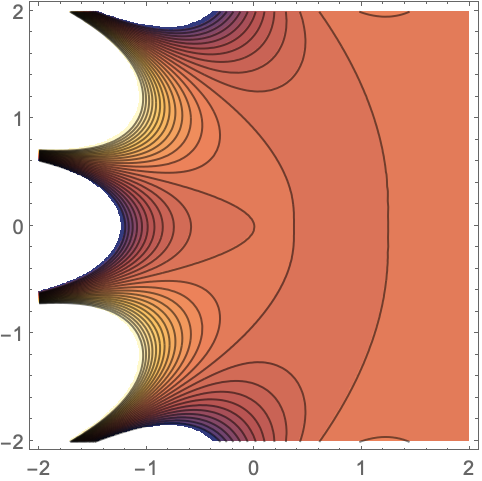
Plot as real parts of two parameters vary:
https://wolfram.com/xid/0j49rir4-elqrq8
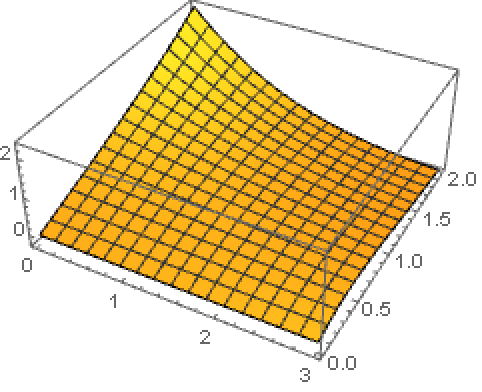
Function Properties (11)
https://wolfram.com/xid/0j49rir4-cl7ele
Complex domain of WhittakerM:
https://wolfram.com/xid/0j49rir4-de3irc
https://wolfram.com/xid/0j49rir4-pugwvl
WhittakerM may reduce to simpler functions:
https://wolfram.com/xid/0j49rir4-bm44p7
https://wolfram.com/xid/0j49rir4-b8hemb
![]() is not an analytic function of
is not an analytic function of ![]() for integer values of
for integer values of ![]() :
:
https://wolfram.com/xid/0j49rir4-h5x4l2
https://wolfram.com/xid/0j49rir4-5fz4kz
It is analytic for other values of ![]() :
:
https://wolfram.com/xid/0j49rir4-1tvuzk
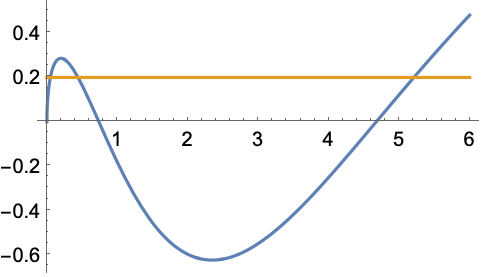
![]() is neither non-decreasing nor non-increasing:
is neither non-decreasing nor non-increasing:
https://wolfram.com/xid/0j49rir4-o1mnqv
https://wolfram.com/xid/0j49rir4-fxi9f9
https://wolfram.com/xid/0j49rir4-zf7zy
https://wolfram.com/xid/0j49rir4-la4so0
https://wolfram.com/xid/0j49rir4-unklza
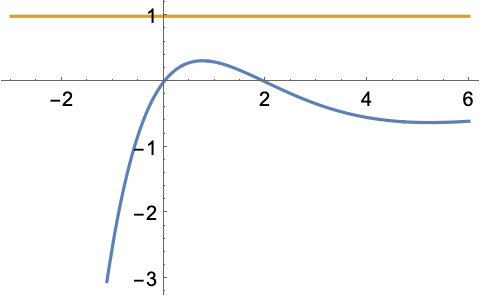
![]() is neither non-negative nor non-positive on its real domain:
is neither non-negative nor non-positive on its real domain:
https://wolfram.com/xid/0j49rir4-7w275t
WhittakerM has both singularity and discontinuity in (-∞,0]:
https://wolfram.com/xid/0j49rir4-1zvsit
https://wolfram.com/xid/0j49rir4-y8p27s
![]() is neither convex nor concave on its real domain:
is neither convex nor concave on its real domain:
https://wolfram.com/xid/0j49rir4-xza3wn
TraditionalForm formatting:
https://wolfram.com/xid/0j49rir4-k6az4l
Differentiation (3)
First derivative with respect to z:
https://wolfram.com/xid/0j49rir4-krpoah
Higher derivatives with respect to z when k=1/3 and m=1/2:
https://wolfram.com/xid/0j49rir4-z33jv
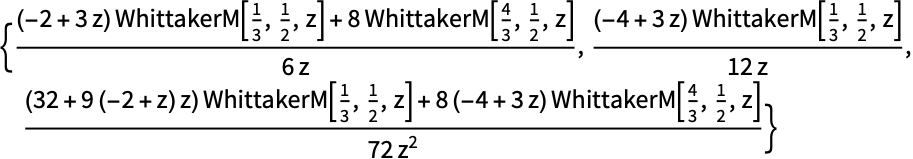
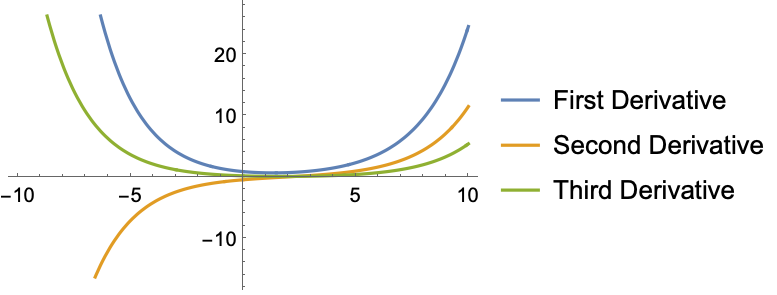
Plot the higher derivatives with respect to z when k=1/3 and m=1/2:
https://wolfram.com/xid/0j49rir4-fxwmfc
Formula for the ![]()
![]() derivative with respect to z:
derivative with respect to z:
https://wolfram.com/xid/0j49rir4-cb5zgj
Series Expansions (5)
Find the Taylor expansion using Series:
https://wolfram.com/xid/0j49rir4-ewr1h8
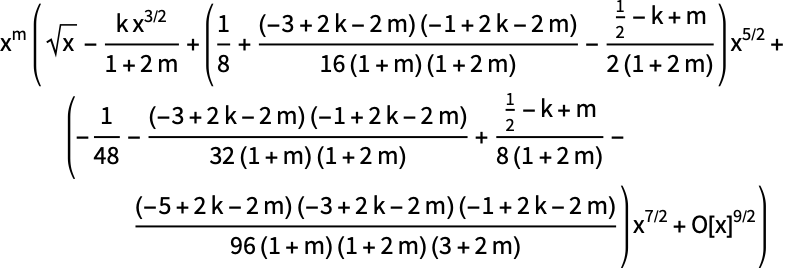
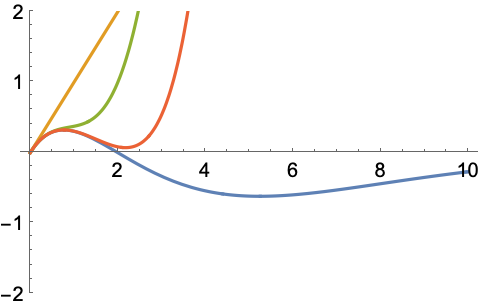
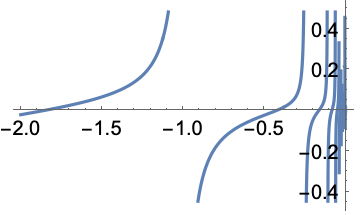
Plots of the first three approximations around ![]() :
:
https://wolfram.com/xid/0j49rir4-binhar
General term in the series expansion using SeriesCoefficient:
https://wolfram.com/xid/0j49rir4-dznx2j
Find the series expansion at Infinity:
https://wolfram.com/xid/0j49rir4-syq
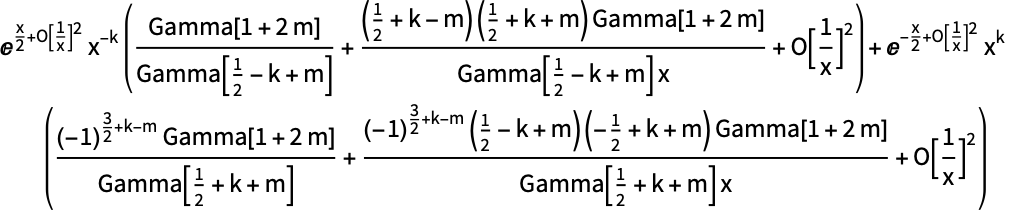
Find series expansion for an arbitrary symbolic direction ![]() :
:
https://wolfram.com/xid/0j49rir4-t5t

Taylor expansion at a generic point:
https://wolfram.com/xid/0j49rir4-jwxla7

Applications (2)Sample problems that can be solved with this function
The bound-state Coulomb eigenfunction in parabolic coordinates:
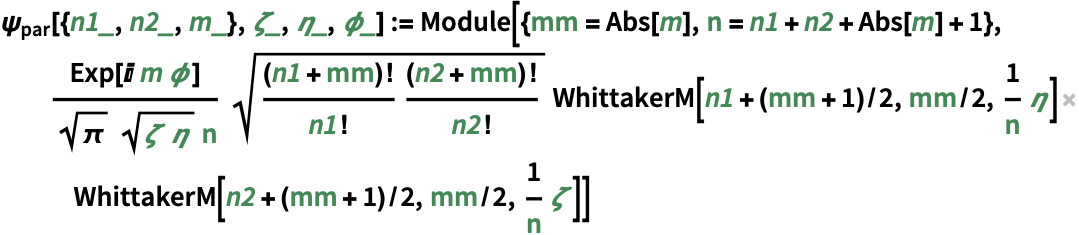
https://wolfram.com/xid/0j49rir4-bvcaux
Decompose the eigenfunction in terms of spherical eigenfunctions:
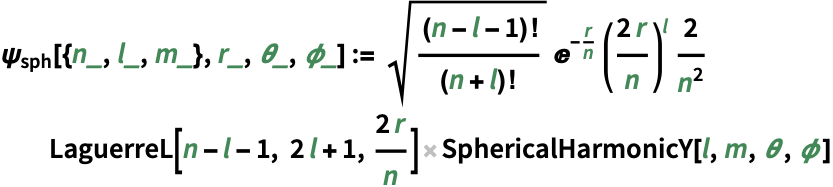
https://wolfram.com/xid/0j49rir4-gmpxzy
Parabolic coordinates relate to radial coordinates as ![]() and
and ![]() :
:
https://wolfram.com/xid/0j49rir4-et42z9
https://wolfram.com/xid/0j49rir4-dndrzs
Green's function of the 3D Coulomb potential:

https://wolfram.com/xid/0j49rir4-edo33e
https://wolfram.com/xid/0j49rir4-fz0c01
Properties & Relations (4)Properties of the function, and connections to other functions
Use FunctionExpand to expand WhittakerM into other functions:
https://wolfram.com/xid/0j49rir4-zktra
https://wolfram.com/xid/0j49rir4-g6xk8e
https://wolfram.com/xid/0j49rir4-e0dc9e
Integrate expressions involving Whittaker functions:
https://wolfram.com/xid/0j49rir4-fcfb3b
WhittakerM can be represented as a DifferentialRoot:
https://wolfram.com/xid/0j49rir4-burqaq
WhittakerM can be represented as a DifferenceRoot:
https://wolfram.com/xid/0j49rir4-dn1ebz
https://wolfram.com/xid/0j49rir4-hn6zh1
Wolfram Research (2007), WhittakerM, Wolfram Language function, https://reference.wolfram.com/language/ref/WhittakerM.html.Text
Wolfram Research (2007), WhittakerM, Wolfram Language function, https://reference.wolfram.com/language/ref/WhittakerM.html.
Wolfram Research (2007), WhittakerM, Wolfram Language function, https://reference.wolfram.com/language/ref/WhittakerM.html.CMS
Wolfram Language. 2007. "WhittakerM." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WhittakerM.html.
Wolfram Language. 2007. "WhittakerM." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WhittakerM.html.APA
Wolfram Language. (2007). WhittakerM. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WhittakerM.html
Wolfram Language. (2007). WhittakerM. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WhittakerM.htmlBibTeX
@misc{reference.wolfram_2025_whittakerm, author="Wolfram Research", title="{WhittakerM}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/WhittakerM.html}", note=[Accessed: 23-June-2025
]}BibLaTeX
@online{reference.wolfram_2025_whittakerm, organization={Wolfram Research}, title={WhittakerM}, year={2007}, url={https://reference.wolfram.com/language/ref/WhittakerM.html}, note=[Accessed: 23-June-2025
]}