WilksW
WilksW[m1,m2]
行列 m1と m2についてWilksの を与える.
詳細
- WilksW[m1,m2]は m1 m2間のWilksの を与える.
- Wilksの は合併共分散行列に基づいた線形従属の尺度である.
- Wilksの は
![1-TemplateBox[{Sigma}, Det]/(TemplateBox[{{Sigma, _, {(, 11, )}}}, Det] TemplateBox[{{Sigma, _, {(, 22, )}}}, Det]) 1-TemplateBox[{Sigma}, Det]/(TemplateBox[{{Sigma, _, {(, 11, )}}}, Det] TemplateBox[{{Sigma, _, {(, 22, )}}}, Det])](Files/WilksW.ja/1.png) として計算される.ただし,
として計算される.ただし,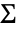 は合併サンプル共分散行列である.このサンプルは
は合併サンプル共分散行列である.このサンプルは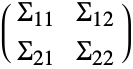 と分割することができる.
と分割することができる.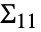 と
と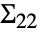 は個々のデータ集合の共分散行列に対応する.
は個々のデータ集合の共分散行列に対応する. - 引数 m1と m2は任意の長さが等しい実行列または実ベクトルでよい.
例題
すべて開くすべて閉じるスコープ (3)
特性と関係 (3)
HoeffdingDを使うとある種の非線形従属構造が検出できる:
の統計的有意性はWilksWTestで検定することができる:
あるいは,IndependenceTestを使って自動的に検定を選ぶこともできる:
Wolfram Research (2012), WilksW, Wolfram言語関数, https://reference.wolfram.com/language/ref/WilksW.html.
テキスト
Wolfram Research (2012), WilksW, Wolfram言語関数, https://reference.wolfram.com/language/ref/WilksW.html.
CMS
Wolfram Language. 2012. "WilksW." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WilksW.html.
APA
Wolfram Language. (2012). WilksW. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WilksW.html