"Isomap" (機械学習メソッド)

詳細とサブオプション

  • "Isomap"は，等長写像を表すもので，非線形の近傍に基づいた次元削減メソッドである．このメソッドは，測地距離を保存する変換を介してデータの低次元埋め込みを見付けようとする
  • "Isomap"は非線形多様体について学ぶことができる．しかし，計算コストが高く，データに高密度の変動がある場合では失敗することがあり，境界についてはあまりよい結果は与えられない．
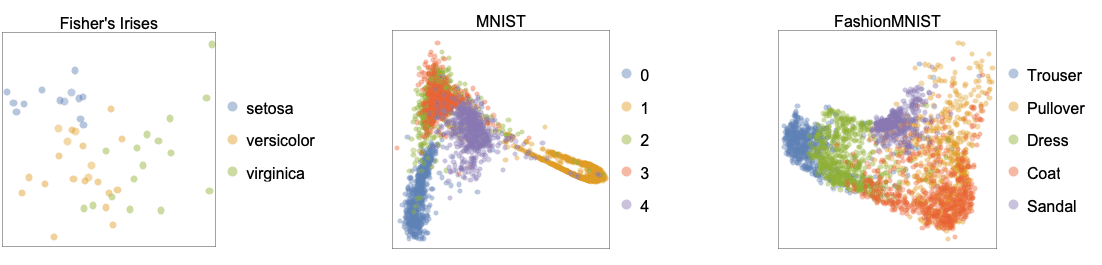
  • 次のプロットは，"Isomap"が学んだ二次元埋込みを，Fisher's Irises，MNIST，FashionMNISTのベンチマークデータ集合に適用した結果を示している．
  • "Isomap"は，まず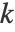， 最近傍が与えられると 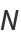N 個のデータ点上に近傍グラフを構築する．多様体上のすべての点のペア間の測地距離は最近傍グラフ 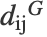内の最短経路距離を推測することで求められる．これは，結果としてグラフ距離 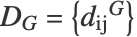の行列になる．このメソッドは，ユークリッド距離（最短距離）が測地距離になる埋込みを求めようとする．低次元埋込み 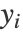は埋込みコストを最低にすることで計算される．min ∑ Ni=1 [||yi-yj||- dijG]2
  • このメソッドは，古典的な"MultidimensionalScaling"をグラフ距離 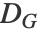の行列に行うことに等しい．したがって，埋込み空間におけるユークリッド距離はグラフ距離と一致する．||yi-yj||≈ dijG
  • 次は，使用可能なサブオプションである．
  • "NeighborsNumber" Automatic近傍 k の数

例題

すべて開くすべて閉じる

例  (1)

「スイスロール」のようなデータ集合を作成し，可視化する：

データ集合に"Isomap"を使って二次元空間にマッピングして，非線形次元削減を訓練する：

削減された空間内のデータ座標を求め，可視化する：

もとの空間内のデータ集合を，各点をその削減された変数に従って彩色して可視化する：

スコープ  (1)

データ集合の可視化  (1)

ExampleDataからFisherのアヤメに関するデータ集合をロードする：

"Isomap"と各例の特徴を使って削減関数を生成する：

例を種によってグループ化する：

特徴の次元を削減する：

削減されたデータ集合を可視化する：

オプション  (1)

"NeighborsNumber"  (1)

3D幾何データから，ランダムな視点によるさまざまな頭部の向きのデータ集合を生成する：

さまざまな頭部の向きを可視化する：

等角写像を実行するために，近傍グラフで"NeighborsNumber"を指定することで，このデータ集合を二次元表現に削減する：

上下と前横の向きのもつれが解消された削減空間でもとの画像を可視化する：