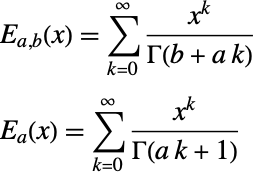分数階微積分学
はじめに
分数階微積分学は任意の実数階または複素数階の微積分の理論を進展させる．これは従来の微積分の基本的な操作を分数階にまで拡張し，このような分数階の微分や積分を含む微分方程式を解く方法を研究するものである[1]．
分数階微積分学はただの純数学理論ではない．これは拡散問題，流体力学，制御理論，信号処理等の分野で人気が高まってきている．多数の科学現象は分数階の微分方程式，積分方程式，混合型方程式で説明が付く．このトピックの重要性と潜在性を認識して，Wolfram言語で分数階微積分学の環境を調べるための関数が開発された．
つまり，分数階微積分はどのような積分方程式や微分方程式でも，対応する「分数階」の無限集合（分数階積分と分数階微分が関含まれる）に一般化することができるのである．したがって，分数階微積分学は新しい物理現象を説明し，既存のモデルの正確性を向上させる可能性を広げる．
分数階微積分学の略歴
整数次の微分と積分が微積分の2つの基本的な操作であった微積分の基礎は，17世紀にニュートン(Newton)とライプニッツ(Leibniz)によって確立された．
1695年にライプニッツはロピタル(L’Hôpital)へのメッセージの中で，「1/2」階微分の意味について書いていた．1823年と1826年にニールス・アーベル(Niels Abel)が書いた2つの論文がこの分数階微積分理論に衝撃を与えた．この論文の中には理論のすべての要素が含まれていたのである．例えば，分数階微分と分数階積分の考え，それらは互いに逆の関係にあること，分数階微分と分数階積分は一般化された同じ操作と見なすことができるということの理解等である．
アーベルは，積分方程式 
を距離 
からの関数として指定された通過時間関数 
について解く，等時曲線問題（アーベルの問題）を一般化することを考えた．未知の関数
を決定することで等時曲線自体の方程式を求めることが可能になる．
代数操作をいくつか経ると，この積分方程式は
という形式で書き換えることができる．これが現在Caputoの1/2階の分数階微分と呼ばれるものである[2]．
20世紀後半まで，分数階微積分学は主に抽象的な数学理論として発展した．さまざまな分野や専門知識を持つ科学者が多様な視点から分数階微積分学とその応用方法について考えてこの理論を使ったため，分数階微積分学はここ数十年で実践的に適用されるようになった．したがって分数階「微積分」操作を定義する方法はさまざまであるが，そのうちの3つがよく使われる．
分数階微積分学とは？
積分は実質的に微分の反対の操作なので，微分と積分が統合された一つの操作，いわゆる「微積分」を定義することができる．文献ではこれは 
と書かれる．ここで微積分の次数はパラメータ
で与えられる．理論上これは任意の実数または複素数である．これが正の整数の場合は常微分に，負の整数の場合は常積分になる．
また，分数階微積分は点 
（下限）における関数 
の値に依存する．それは関数の「歴史」を表す追加のパラメータである．実際には，下限は通常0なので，分数階の微分・積分は原点における関数の値を含んでいる．これは初期値問題を解く際に便利である．
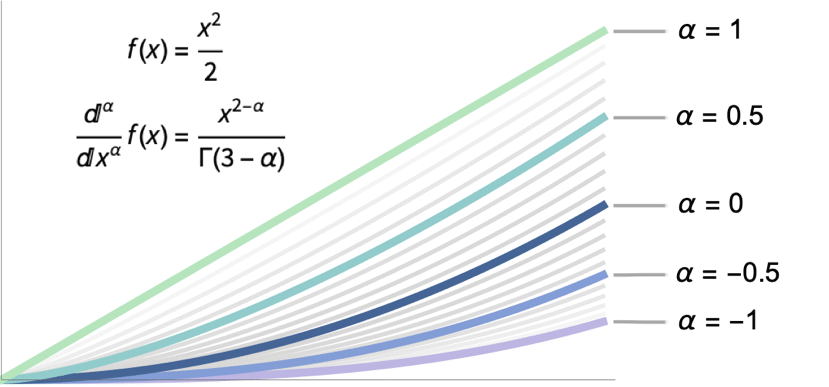
分数階微積分理論で最も重要な出発点は，分数階の微積分演算子の定義に関係なく，微積分は整数
の常微分／積分と一致しなければならないということである．下の図では二乗関数，その常微分，常積分，分数階微分，分数階積分が示されている：
二乗関数の指数階微分
二乗関数 
の一階微分は 
であり，その積分は 
であることはよく知られているが，この関数の1/2階微分は何であろうか．または反対の操作である，関数の積分は何であろうか．
この項式に負の 
を置くと，この関数の 
階不定積分が簡単に得られる：
後者の関数の 
階常微分を取りそれに
を代入すると以下が得られる：
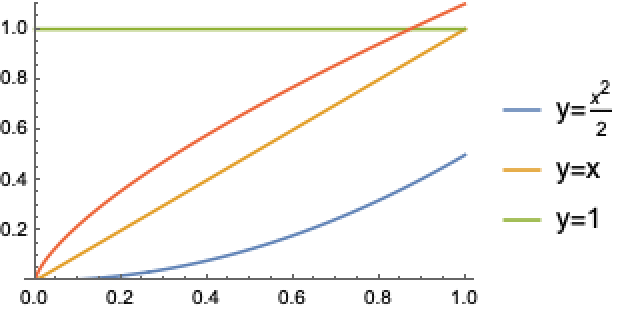
明らかにこれは「1/2階微分」を2階行うことで得られた，二乗関数の一階微分である．さらに，同様の1/2階積分操作（先に示した公式で
を代入する）を2回行うことによって二乗関数の定積分が得られることも簡単に検証できる．上に示した操作は，二乗関数の分数階微積分に他ならない．
分数階微積分の定義
1. グリュンバルト・レトニコフ(Grünwald–Letnikov)アプローチ． グリュンバルト・レトニコフ微積分 は明らかに従来の微分・積分の拡張を与え，極限に基づいている：
実際，このアプローチはさまざまな点において無限数の関数の近似を含んでいるため，あまり使いものにならない．それを計算する高度なアルゴリズムもあるが[3]，実践面で計算的に高価になる：
2. リーマン・リウヴィル(Riemann–Liouville)微積分． リーマン・リウヴィルの定義 は以下である：
リーマン・リウヴィルのアプローチは，分数階微積分学の厳密な数学的理論の根底にある．この理論は十分に発展しているが，リーマン・リウヴィルのアプローチには，現実世界の問題に応用するにはそれほど適していないものとするような制約がある．しかしこの理論は理論的側面にとっては非常に重要である．
3. Caputo 微積分． Caputoの定義は以下である：
これとリーマン・リウヴィル微積分の間には類似性がある．実際Caputo微積分はリーマン・リウヴィルアプローチで定義することができる：
この定義によると，Caputoの分数階微分は，負の次数 
についてのリーマン・リウヴィルの分数階微分に一致する．
Caputoによる微積分の定義には，リーマン・リウヴィルやグリュンバルト・レトニコフの定義と比べて優れた点が多い．まず，Caputoの定義は関数の値と原点（一般に任意の下限点 
）におけるその微分を考慮に入れている．このことによって，ラプラス変換を使って分数階初期値問題を解くのに自動的に適したものとなる．また，「定数」についてのCaputoの分数階微分はゼロ（一般の分数階微分はゼロではない）なので，従来の微積分学とより一貫性がある．
以下のアニメーションは二乗関数についてのCaputoの分数階微分の動作を常微分と比較して示している．見ての通り，分数階微分は整数階の間を「補間」し，整数階の微積分については常微分と一致する：
Wolfram言語における微積分
Wolfram言語にはFractionalD関数とCaputoD関数が含まれており，それぞれリーマン・リウヴィルの分数階微積分とCaputoの分数階微積分[4-5]を表している．これらの関数は分数階微分
および 
を記号的に計算する．
FractionalD関数
次は分数階微分の規則がどのように導出されるかを示す簡単な例である．三次関数の1/2階微分はリーマン・リウヴィルの定義を使って計算される：
上の入力は，分数階微積分についてのリーマン・リウヴィルの定義を直接適用したにすぎない．ここでこの結果を組込みのFractionalD関数を使って検証する：
次の計算は，ネストされた3つの分数階積分（常積分は1/3階積分3回と同じである）を使って最初の関数を回復する：
この三次関数の任意の分数階微分を計算し，特定の階数の表を作成して微分のリストをプロットする：次に
次にExp関数とBesselJ関数の0.23階微分を計算する：
MeijerGの分数階微分は，別のMeijerG関数で与えられる：
上の例は非常に重要な理論的特徴であり，別の組込みのMeijerGReduce関数によって得られたMeijerG表現を使って複素関数のFractionalD規則を作成するために使うことができる．
最後の例として，いくつかの一般的な特殊関数に対する 
階リーマン・リウヴィル微分と 
階常微分の表を示す：
CaputoD関数
CaputoD関数はCaputo分数階derivative 
を与える．これは理論的定義に基づいて原点における関数の値を考慮に入れるため，現実世界での応用にはより便利な関数と言える．
基本的で重要な特徴の一つに，定数のCaputo分数階微分は0になる（リーマン・リウヴィル微分はならない）というものがある：
階数 
が負の場合，CaputoDの出力はFractionalDと一致する．これはその定義によるためだけに起こる：
ここでExp関数の0.23階Caputo微分を計算する：
BesselJ関数の1/2階Caputo微分を計算する：
最後の例として，いくつかの一般的な数学関数の1/2階Caputo微分を示す：
数値分数階微積分
FractionalDとCaputoDは重要であり非常に強力な関数であるが，その複雑な定義（関数掛ける別のベキ乗関数の積分の微分または微分の積分）のため，計算に時間がかかり厄介な出力が出る可能性がある．あるいは入力のクラスが幅広くなると組込みの積分メソッドでは出力が生成できないこともある．次の例ではFractionalDが，DifferenceRoot関数によって与えられる汎用ホロノミック数列を含む出力を生成する：
そのような記号関数の数値版があると便利である．Integrateにはその数値版のNIntegrateがあり，DSolveにはNDSolveがある．同様にFractionalDとCaputoDには[1]と[3]で示された異なるアルゴリズムに基づくそれぞれの数値版NFractionalD関数とNCaputoD関数がある．これらの関数の設計は簡単である．これらは指定された点における指定された階数の分数階微分の値に対応する数値出力を生成するだけである．次の例では，点
における二乗関数の1/2階微分の値を計算する：
これらの関数を使うと，分数階微分の動作への洞察（プロットする等）が得られる．例として，出力にDifferenceRootを持つ，この章の最初の出力を考える．一般的には，
関数の分数階微分にどの関数が関わっているかは知られていない．しかしこの分数階微分をNFractionalD関数またはNCaputoD関数でプロットすることで，ある程度の理解を得ることができる：
NCaputoD関数を含む別の例である：
また，分数階微分および分数階積分に対するグリュンバルト・レトニコフアプローチはNFractionalDで利用できる：
分数階微分のラプラス(Laplace)変換
ラプラス変換と関数とMittagLefflerE関数は分数階の微分および積分を含む微分方程式の解法において重要な役割を果たす．以下ではMittagLefflerEについての基本情報およびLaplaceTransformを使った分数階微分方程式の解法を示す．
MittagLefflerE関数は指数関数の自然な一般化である．「定数係数の常微分方程式」が指数関数で解かれるように，「定数係数の分数か微分方程式はMittagLefflerE関数で解かれる．次は通常のMittagLefflerE関数と一般化されたMittagLefflerE関数の定義である：
指数関数はMittagLefflerEの特殊形である：
MittagLefflerE関数のラプラス変換はWolfram言語を使って計算することができる：
LaplaceTransformは時間領域のMittagLefflerEを 
領域とも言われる周波数領域に変換することができる：
この周波数領域の関数には，極および負の無限大から実軸の原点までの分岐切断が見られる：
InverseLaplaceTransformを適用すると，もとのMittag–Leffler関数が復元される：
領域の関数のクラスはすべて，Mittag–Leffler関数を含む 
領域の式に変換された逆ラプラスである：
LaplaceTransformを使うと，最初の 
領域関数が復元できる：
整数階微分に対するラプラス変換は，整数階微分方程式を解くのに重要な役割を果たすことはよく知られている．これは，例えば，2階微分のLaplaceTransformがその関数のLaplaceTransformで表せるからである：
分数階微分のLaplaceTransformにも同じ特性がある．例えば，次は3/2階CaputoD微分のLaplaceTransformである：
この特性を使うと，正弦関数のCaputo微分のラプラス変換が計算できる：
まず正弦関数のCaputoDを計算してから，その出力にLaplaceTransformを適用しても同じ結果が得られる：
最初のアプローチの利点は，Sin関数のLaplaceTransformを計算するだけでよいという点である．2つ目のアプローチではSinのCaputoDで発生する複雑なHypergeometricPFQ関数のLaplaceTransformを求めなければならない．
分数階微分方程式
分数階微分方程式(FDE)は分数階微分 
を含む微分方程式のことである．分数階微分方程式は，工学，物理，化学，生物学，その他の分野で広く使われ注目されてきた常微分方程式(ODE)の一般化である．
最初のステップとして，定数係数を持つ線形の分数階常微分方程式を考える．常微分方程式の場合と同様に，LaplaceTransformを使って最初の分数階微分方程式を 
次元の代数方程式に変換し，それを解くことができる．それからInverseLaplaceTransformを使って，最初の分数階微分方程式の時間領域の解を復元する．以下にこのプロセスを示す．
まずいくつかの初期値で，LaplaceTransformを分数階微分方程式の両辺に適用する：
LaplaceTransformについて解く：
最後にInverseLaplaceTransformを適用して時間領域の解を求める：
この解はDSolveを使って直接導くことができる：
DSolveは「定数係数を持つ任意の分数階微分方程式」を解くことができる．次は1/2階微分方程式の例である：
Caputo型の分数階微分方程式の場合，初期条件は整数階微分に対して与えられる．初期条件の数は分数階微分方程式の階数 
に依存し，
に等しい．以下は前の例の初期値問題の解である：
次の例は，4個の初期条件を含む階数 
の分数階微分方程式を解く：
DSolveは定数係数の線形分数階微分方程式系も扱うことができる．以下のように，系の方程式はすべて 
の同じ階数を持たなければならない：
最後の例として，ベクトル変数を使った3つの分数階微分方程式系の解を考える：
応用
近年分数階微積分学は科学のさまざまな分野でますます応用されるようになってきた．以下にいくつか例を挙げる．
分数調波発振器
この分数調波発振器の挙動は，通常の減衰調和振動子の挙動に非常に似ている：
分数調波発振器と減衰調和振動子の解をプロットし，それらを比較する：
この例によって，分数階微分方程式の階数は，複雑な系をモデル化するための制御パラメータとして使うことができるということが明らかに分かる．
分数減衰を含む力学系
広いニュートン流体に浸された，密度 
，粘弾性定数 
，質量 
，面積 
の薄いプレートで構成される力学系を考える．このプレートはバネ係数 
のバネで固定点と繋がっている．プレートの表面は液体によってプレートの動きが遅くなるほどの大きさがあるものと仮定する．
この系はパラメータ 
および 
を使って，分数減衰を持つ二階微分方程式でモデル化することができる[6]：
パラメータ値 
，
で階段状の力 
についてモデル方程式を解き，解をプロットする：
分数分周LC回路
の場合，これは分数の一般化モデルを与え，その解は以下になる：
分数RC回路
分数波動方程式
DSolveで解くことができる：
まとめ
分数階微積分学は，有名な積分微分方程式をターゲットとなる関数の分数階微分または分数階積分を含む方程式に一般化することができるため，今日ますます注目を集めている．方程式が一般的であるほど，異なる現実世界の減少をより正確に描写することができるのである．
この潜在性を考慮して，Wolfram言語には分数階微積分学の基本的な2つの演算子，FractionalD関数とCaputoD関数が含まれている．また，DSolveでLaplaceTransformを使って分数階微分方程式の解法をサポートするために，多大な開発努力がなされた．
Wolfram言語には，NFractionalDとNCaputoDを使った分数階微積分の数値サポートも含まれている．NFractionalDにはリーマン・リウヴィルアプローチとグリュンバルト・レトニコフアプローチを表す2つの内部メソッドがあり，ほとんどの実践的応用にはこれで十分である．
参考文献
1. Oldham, K. B. and J. Spanier. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order. Academic Press, 1974.
2. Podlubny, I., Magin, R. and I. Trymorush. "Niels Henrik Abel and the Birth of Fractional Calculus." Fractional Calculus and Applied Analysis 20, no. 5 (2017): pp. 1068–1075.
3. Li, C. and M. Cai. Theory and Numerical Approximations of Fractional Integrals and Derivatives. SIAM, 2019.
4. New in Wolfram Language 13.1 webinar series.
5. T. Ishkhanyan. "Fractional Calculus in Wolfram Language 13.1" blog post.
6. Kilbas A., Srivastava, H. M. and J. J. Trujillo. Theory and Applications of Fractional Differential Equations. Elsevier, 2006.