置換

置換表現置換の積
置換の作用と台置換の等価性と並替え
式の一部を置換する特殊なタイプの置換
置換は代数における基本的な要素である．行列と同様に，置換には自然な非可換積があるため，非常に非自明な構造を簡潔に符号化することができる．置換は任意の有限群を表す方法を提供するということにより，数学，科学，工学，さらには芸術における多数のアプリケーションの主要ツールとなっている．特に置換は離散対称性の記述で中心的な役割を果たしている．
大まかに言うと置換は元の集合の並替えであるが，正確にはその集合からそれ自身への全単射である．有限数の元を持つ集合のみを考える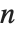． 個の元を持つ集合で可能な置換の数は 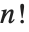である．したがって，例えば のとき通り，つまり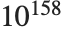通りの置換があるということである．
このチュートリアルではWolfram言語における巡回表記の置換の操作方法を説明し，「置換のリスト」では置換リスト表記との関連性を説明する．また，「置換群」では置換群の一般論を，「名前付き群」では置換群の中のいくつかの特殊な群について説明する．「群論アルゴリズム」では群の元をすべて列挙しないで置換群から情報を抽出する方法を見てみる．
置換表現
Cycles
互いに素な巡回置換を表す頭部
PermutationCyclesQ
置換の検証
置換表現
置換の互いに素な巡回表現は，Wolfram言語ではCycles[{cyc1,cyc2,…}]という形式を持つ．ここで巡回 cyci は互いに素な正の整数のリストである．この置換では整数がその右側に写像され，最後の整数が最初の元に写像される．巡回置換に現れない整数は，長さ1の巡回置換に現れることがあるが，その整数はそれ自身に写像される．これを「一元集合」または「固定点」と呼ぶ．巡回置換の順序は重要ではなく，個々の巡回は置換を変更することなく交代させることができる．置換は自動的に標準化されるため各巡回の最小の整数が最初に来て，巡回置換はその最初の整数によりソートされる．
次は2つの巡回とを持つ置換である：
同じ置換を表す．一元集合と空の巡回置換は除去される：
一元集合のみを持つ置換は恒等置換を表す：
明示的な数値のリストを含む置換では，自動的にシンタックスのチェックが行われる．その他の場合は関数PermutationCyclesQを使ってシンタックスをチェックすることができる．
巡回置換は互いに素でなければならない：
整数は正でなければならない：
整数以外の数値は使えない：
次は有効な巡回置換である：
以下は明らかに無効な置換である：
置換の作用と台
置換 perm により，整数 が整数 にマップされると，「 は置換 perm による の像」という．像は関数PermutationReplaceで計算される．
PermutationReplace
置換による整数の像
他の式に対する置換の標準的作用
次は3の像である：
最初の6つの整数の像である：
置換の標準的な作用は，他の置換や整数の配列のように別のオブジェクトにまで拡張することができる．
2つ目の置換により最初の置換の整数をマップする（共役作用）：
置換は特定のどの有限群にも属さず，ある程度特定の対称群にさえ属さないとされている．しかし置換により動かされた整数の集合として定義された，台という概念があり，これにより置換が自然に作用を及ぼす場所がより分かる．
PermutationSupport
置換によって動かされた整数集合
PermutationLength
置換によって動かされた整数の数
PermutationMax
置換によって動かされた最大の整数
PermutationMin
置換によって動かされた最小の整数
置換の台関数
次の置換は5つの点だけを動かす：
動いた点で最大のものは55である：
動いた点で最小のものは4である：
RandomPermutation
擬似ランダム置換を生成する
置換のランダムな生成
整数{1,…,15}を動かす（すべてとは限らない）ことでランダム置換を生成する：
指定された群でいくつかのランダム置換を生成する：
式の一部を置換する
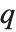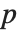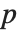置換は，関数Permuteを使って他の式の一部を置換するのにも使える．整数 に写像される整数 は， が 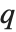の位置に動かされるものと解釈される．Permuteは式の元の数は決して変更しない．ただ順序が変わるだけである．
Permute
式の一部を置換する
FindPermutation
2つの式を同じ元でつなぐ置換を返す
置換での並べ替え
アルファベットの最初と最後の文字を入れ替える：
式の3つの部分を置換し，残りはそのままにしておく：
置換リスト表現と関数Partを使うと同じ結果が得られる：
しかし，置換リストの長さは式の長さにマッチしていなければならない：
置換リストは関数Permuteで使うこともできる：
それとは逆に，同じ元を持つ2つの式があるとすると，それらを連結する置換を計算することができる：
2つの引数を入れ替えると，逆置換になる：
引数が1つだと，FindPermutationは式を標準的な順番から生成する置換を返す：
置換の積
PermutationProduct
置換の積（非可換）
InversePermutation
逆置換
PermutationPower
置換の整数ベキ（自身あるいは逆置換との積）
PermutationOrder
恒等置換を生成する，置換の最小の正のベキ
置換の積
2つの置換 perm1と perm2の積を求める場合，PermutationProduct[perm1,perm2]が perm1を使ってから perm2を使う（左から右への積）か，perm2を使ってから perm1を使う（右から左への積）かによって決まる，2通りの方法が考えられる．Wolfram言語のPermutationProductでは巡回の右隣に写像することになっているため，実質的に左から右への積である．
置換の積は可換ではない：
PermutationReplaceは，積の左から右という性質と矛盾することなく，右から作用する：
Permuteは右から作用することもある：
置換の積の法則が与えられると，転置，ベキ乗，位数等の関連した概念がすぐに定義できる．有限の台の置換では，位数は常に有限となる．
逆置換を計算することができる：
それをベキ乗する．負のベキ乗は逆置換のベキである：
置換の位数は，恒等置換を得るような最低の正のベキである：
別の例：
次は，有限の台の置換では逆置換は常に置換の正のベキ乗となるということを意味している：
置換の等価性と並替え
Wolfram言語の標準となっているが，等価性テストには構造的等価性(SameQ)と数学的等価性(Equal)の2つがある．前者は2つの式を比較することができるが，後者は同じタイプの値を持つ2つの数式を比べた場合にのみTrueかFalseを返す．式を並べ替えるときも同じである．OrderおよびOrderedQで実装された構造的（標準的）順序とLessとその関連関数で与えられる数学的順序がある．
任意位数の2つの置換は常にその等価性と順序をテストすることができる．これは整数1, 2, 3, …の像を逐次に比較することによって実行される．恒等置換が常に最初に来るように小さい置換は小さい像に対応する．これは数学的順序を定義する．標準的順序は標準の規則に従っており，数学的順序とは異なる可能性がある，
2つの置換を取る：
それぞれの置換による，最初の7つの整数の像である：
置換perm2の2番目の像の方が小さいので，perm2はperm1の前に並べ替えなければならない：
標準的な順序では，小さい式から並べ替える：
並替え関数を使うことで，置換を数学的順序で並べ替えることができる：
置換のリストがソートされているかどうかをチェックすることができる：
特殊なタイプの置換
置換には特殊なタイプがある．多くの場合，巡回表記により簡単な構造でタイプを見付けることができる．
対合には最大長2の巡回置換のみが含まれる：
すべての整数が動いたら，置換は位数 の乱列である：
1つの長さ の巡回置換からなる場合，その置換は位数 の円順列と言われる：
置換の巡回表記を互換へと分解すること，つまり長さ2の1つの巡回を持つ置換を構築することも簡単である．
次の関数は，積がもとの置換となるような互換のリストを構築する：
このような互換への分解は一意的ではないが，互換の数のパリティ（偶か奇）は不変である．これは置換の符号と呼ばれる：
前の例では，置換 perm は5つ，つまり奇数の互換に分解された．したがってこれには符号-1がある：