置换

一个置换的表示置换的积
置换作用和支撑置换的相等和排序
置换一个表达式的某些部分置换的特殊类型
置换是代数中的基本元素. 它们有自然的非交换乘积（像矩阵那样），因而可以以紧凑的方式为高度非平庸的结构编码. 置换提供了一种可以表示任何有限群的方法，使之成为在数学、科学、工程甚至艺术等领域许多应用中的关键工具. 特别地，置换在离散对称性的描述中起核心作用.
置换，粗略地说，就是对一个集合的元素进行重新排列，更精确地说，是一个集合到它本身的一一对应. 这里仅考虑元素数目有限的集合. 一个 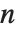元素的集合的可能置换数是 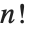，所以即使对中等数目 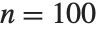，就已经有，即差不多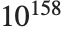 个置换了.
本教程讨论在 Wolfram 语言中如何用轮换表示法来对置换进行操作. 另一教程 "置换列表" 则描述其与置换列表表示法的关系. 然后，其它的教程 "置换群" 和 "已命名的群" 描述如何处理置换群，"群论算法" 阐明如何在不用列出所有群元的情况下获取有关信息 .
一个置换的表示
Cycles
以不相交轮换的形式表示一个置换时的头部
PermutationCyclesQ
验证一个置换
置换的表示.
在 Wolfram 语言中，一个置换的不相交轮换表示具有形式 Cycles[{cyc1,cyc2,…}]，其中，cyci 是正整数的不相交列表. 在置换下，整数被映射到它们的右邻，而最后一个整数被映射到那个轮换的第一个数. 不在轮换内的整数被映射到它们本身，虽然它们也可以以长度为一的轮换的形式出现. 这种轮换称为 singletons（单元集）或 fixed points. 轮换的排序是无关紧要的，单个的轮换可以进行转动而不致引起置换的改变. 置换是自动正规化的，即每个轮换把最小的整数放在第一位，而所有轮换则按照它们的第一个整数的大小排序.
这是一个有两个轮换 和 的置换：
这里表示的是同一个置换. 单元集和空轮换被排除了：
任何只有单元集的置换代表恒元：
对于包含显式的数字列表的置换，句法会自动得到检查. 其它情况下，用户可以用函数 PermutationCyclesQ 来检查句法.
轮换必须是不相交的：
整数必须是正的：
整数以外的数不被接受：
这是一个以轮换形式表示的有效置换：
很显然，这些都是无效的置换：
置换作用和支撑
如果一个置换 perm 将整数 映射到整数 ，则称 为在置换 perm 下的 像. 像可以用函数 PermutationReplace 来计算.
PermutationReplace
一个置换下一个整数的像
置换在其它表达式上的标准作用.
这是3的像：
这些是前六个整数的像.
置换的标准作用也可以扩展到其它对象上，如其它置换或整数数组.
在第二个置换下对第一个置换的整数作映射（共轭）：
置换并不被看成是属于任何一个特定的有限群，甚至不属于某一次数的特定对称群. 但是有一个称为支撑的概念，它被定义为被置换所移动的整数的集合.
PermutationSupport
被置换所移动的整数的集合
PermutationLength
被置换所移动的整数的数目
PermutationMax
被置换所移动的最大整数
PermutationMin
被置换所移动的最小整数
置换支撑函数.
下面的置换只移动5个点：
被移动的最大的点是55：
被移动的最小的点是4：
RandomPermutation
生成准随机置换
置换的随机生成.
生成一个移动（也许并非全部）整数 {1,…,15} 的随机置换：
在一个给定的群中生成若干个随机置换：
置换一个表达式的某些部分
通过函数 Permute，置换可以用来置换其他表达式的某些部分. 整数 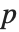被映射到整数 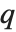这件事被解释为部分 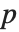被移动到了部分 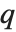. Permute 永远不会改变一个表达式的元素的数目，它只是将它们重新排序.
Permute
置换一个表达式的某些部分
FindPermutation
返回联系两个具有相同元素的表达式的置换
在一个置换下重新排序.
将字母表中的第一个字母和最后一个字母对换：
置换一个表达式中的三个部分，其余的保持不变：
应用一个置换列表表示和函数 Part 可以得到相同的结果：
但是，置换列表的长度必须得与表达式的长度相符：
置换列表也可以和函数 Permute 一起使用：
反过来，给出两个具有相同元素的表达式，可以计算把它们联系起来的一个置换：
反转两个参量将给出逆置换：
当只有一个参量时，FindPermutation 返回这样一个置换：该置换按照其正规排列生成一个表达式.
置换的积
PermutationProduct
置换的乘积（非交换）
InversePermutation
一个置换的逆
PermutationPower
一个置换的整数幂（与自身或逆的乘积）
PermutationOrder
一个置换产生逆的最低正幂
置换的乘积.
对于两个置换 perm1 和 perm2 的乘积有两种可能的约定，取决于 PermutationProduct[perm1,perm2] 是先使用 perm1，然后使用 perm2 （称为从左到右的积），还是先使用 perm2，再使用 perm1 （从右到左的积）. 按照在循环中将图像写为右邻的惯例，Wolfram 语言的 PermutationProduct 实际上是从左到右的积.
置换的乘积是非交换的：
PermutationReplace 从右边作用，与乘积的从左到右特征一致：
Permute 也从右边作用：
置换的乘法规则给出以后，便可立即定义相关的逆、幂、和阶的概念. 对于有限支撑的置换，其阶总是有限的.
可以计算置换的逆：
也可以计算它们的幂. 负幂是其逆的幂：
一个置换的阶是其得到恒元的最低正幂：
另一个例子：
这里表明，（对于有限支撑的置换）逆总是一个置换的正幂：
置换的相等和排序
作为 Wolfram 语言中的标准，有两种类型的相等检验：结构上的相等 (SameQ) 和数学上的相等 (Equal). 前者可以比较任何两个表达式，但后者在比较具有相同数据类型的数学表达式的时候，只返回 True 或 False. 在对表达式进行排序时情形也是一样：有结构上的（正规）次序，这是通过 Order 和 OrderedQ 来实现的；也有数学上的次序，由 Less 及相关函数给出.
任何次数的任何两个置换都可以检验其相等与排序. 这是通过按次序比较整数1、2、3 … 的像来完成的. 较小的置换对应较小的像，所以恒元置换总是排在第一. 这定义了数学上的次序. 正规次序比照标准规则，且有可能与数学上的次序不同.
采用两个置换：
这些是这两个置换下头7个整数的像：
置换 perm2 必须排在 perm1 之前因为它的第二个像较小：
标准的正规排序将首先排较小的表达式：
可以通过用一个“排序函数”（"ordering function"）用数学上的次序对置换进行排序：
你也可以检验一个置换列表是否已经排序：
置换的特殊类型
有一些特殊类型的置换. 在许多情况下，轮换标记允许用简单的构建来检测它们.
对合仅包含最大长度为2的轮换：
一个置换是一个 次重排，如果所有整数 都被移动了：
一个置换被说成是 次循环的，如果它仅包含一个长度为 的轮换
从置换的轮换表示法构造一个对换分解也很简单. 对换是仅有一个长度为2的置换.
这些函数构造一个对换的列表，它们的乘积给出原来的置换：
这样的对换分解不是唯一的，但对换数目的奇偶性不变的. 该奇偶性被称为置换的符号：
前面例子中的置换 perm 被分解为五个对换，是一个奇数，因此它有符号 -1：