ARIMAProcess[{a1,…,ap},d,{b1,…,bq},v]
表示差分整合移动平均自回归过程 ![]() ,其中第
,其中第 ![]() 阶差分是弱平稳 ARMAProcess[{a1,…,ap},{b1,…,bq},v].
阶差分是弱平稳 ARMAProcess[{a1,…,ap},{b1,…,bq},v].
ARIMAProcess[{a1,…,ap},d,{b1,…,bq},Σ]
表示向量 ARIMA 过程 (y1(t),… ,yn(t)),其中第 (d,…,d)![]() 阶差分是向量弱平稳 ARMAProcess.
阶差分是向量弱平稳 ARMAProcess.
ARIMAProcess[{a1,…,ap},{d1,…,dn},{b1,…,bq},Σ]
表示向量 ARIMA 过程 (y1(t),… ,yn(t)),其中第 (d1,…,dn)![]() 阶差分是向量弱平稳 ARMAProcess.
阶差分是向量弱平稳 ARMAProcess.
ARIMAProcess[{a1,…,ap},d,{b1,…,bq},v,init]
表示初始数据为 init 的 ARIMA 过程.
ARIMAProcess[c,…]
表示常量为 c 的 ARIMA 过程.


ARIMAProcess
ARIMAProcess[{a1,…,ap},d,{b1,…,bq},v]
表示差分整合移动平均自回归过程 ![]() ,其中第
,其中第 ![]() 阶差分是弱平稳 ARMAProcess[{a1,…,ap},{b1,…,bq},v].
阶差分是弱平稳 ARMAProcess[{a1,…,ap},{b1,…,bq},v].
ARIMAProcess[{a1,…,ap},d,{b1,…,bq},Σ]
表示向量 ARIMA 过程 (y1(t),… ,yn(t)),其中第 (d,…,d)![]() 阶差分是向量弱平稳 ARMAProcess.
阶差分是向量弱平稳 ARMAProcess.
ARIMAProcess[{a1,…,ap},{d1,…,dn},{b1,…,bq},Σ]
表示向量 ARIMA 过程 (y1(t),… ,yn(t)),其中第 (d1,…,dn)![]() 阶差分是向量弱平稳 ARMAProcess.
阶差分是向量弱平稳 ARMAProcess.
ARIMAProcess[{a1,…,ap},d,{b1,…,bq},v,init]
表示初始数据为 init 的 ARIMA 过程.
ARIMAProcess[c,…]
表示常量为 c 的 ARIMA 过程.
更多信息

- ARIMAProcess 是一个离散时间和连续状态随机过程.
- 对于 d≥1,ARIMAProcess[…,d,…,v] 具有次数为 d 的多项式趋势.
- ARIMA 过程由差分方程
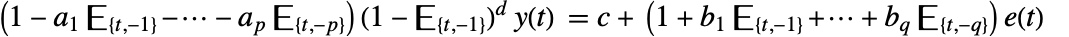 给出,
其中
给出,
其中 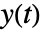 是状态输出,
是状态输出,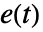 是白噪声输入,而
是白噪声输入,而 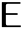 是平移运算符,常数 c 在未指定的情况下取零.
是平移运算符,常数 c 在未指定的情况下取零. - 初始数据 init 可以用列表 {…,y[-2],y[-1]} 或时间标记为 {…,-2,-1} 的单一路径 TemporalData 对象的形式给出.
- 标量 ARIMA 过程应该具有实系数 ai、bj 和 c,非负整数积分阶数 d 以及正方差 v.
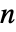 维向量 ARIMA 过程应该具有维度为
维向量 ARIMA 过程应该具有维度为 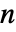 ×
×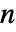 的实系数矩阵 ai 和 bj,长度为
的实系数矩阵 ai 和 bj,长度为 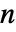 的实向量 c,整数非负积分阶数 di 或者整数非负积分阶数 d,而协方差矩阵 Σ 应该是维度为
的实向量 c,整数非负积分阶数 di 或者整数非负积分阶数 d,而协方差矩阵 Σ 应该是维度为 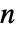 ×
×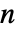 的对称正定矩阵.
的对称正定矩阵.- 常数为零的 ARIMA 过程具有传递函数
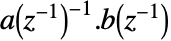 ,其中
,其中 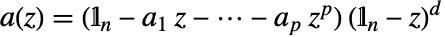 ,
,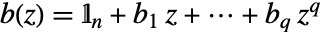 ,其中
,其中 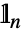 是
是 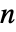 -维单位.
-维单位. - ARIMAProcess[p,d,q] 表示自回归和移动平均阶数为 p 和 q、积分阶数为 d 的 ARIMA 过程,用于 EstimatedProcess 及相关函数.
- ARIMAProcess 可以与诸如 CovarianceFunction、RandomFunction 和 TimeSeriesForecast 等函数结合使用.
范例
打开所有单元 关闭所有单元范围 (25)
基本用法 (9)
使用 TimeSeriesModel 自动求阶数:
估计方法 (5)
估计 ARIMAProcess 的可用方法:
谱估计量允许用于 PowerSpectralDensity 计算的窗:
过程切片性质 (5)
表示法 (4)
StateSpaceModel 表示法:
应用 (3)
数据具有线性趋势,可用 UnitRootTest 来确认:
用 UnitRootTest 求积分阶数:
属性和关系 (4)
ARIMAProcess 是 ARMAProcess 的推广:
ARIMAProcess 是 ARProcess 的推广:
ARIMAProcess 是 MAProcess 的推广:
ARIMA 过程在离散步长服从 WienerProcess:
可能存在的问题 (5)
巧妙范例 (2)
文本
Wolfram Research (2012),ARIMAProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ARIMAProcess.html (更新于 2014 年).
CMS
Wolfram 语言. 2012. "ARIMAProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/ARIMAProcess.html.
APA
Wolfram 语言. (2012). ARIMAProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ARIMAProcess.html 年
BibTeX
@misc{reference.wolfram_2025_arimaprocess, author="Wolfram Research", title="{ARIMAProcess}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ARIMAProcess.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_arimaprocess, organization={Wolfram Research}, title={ARIMAProcess}, year={2014}, url={https://reference.wolfram.com/language/ref/ARIMAProcess.html}, note=[Accessed: 05-February-2026]}