AcousticImpedanceValue
AcousticImpedanceValue[pred,vars,pars]
表示偏微分方程的时域或频域阻抗边界条件,其中谓词 pred 指示其适用位置,模型变量为 vars,且全局参数为 pars.
AcousticImpedanceValue[pred,vars,pars,lkey]
表示时域或频域边界条件,其中局部参数在 pars[lkey] 中指定.
更多信息



- AcousticImpedanceValue 指定 AcousticPDEComponent 的边界条件,并用作建模方程式的一部分:
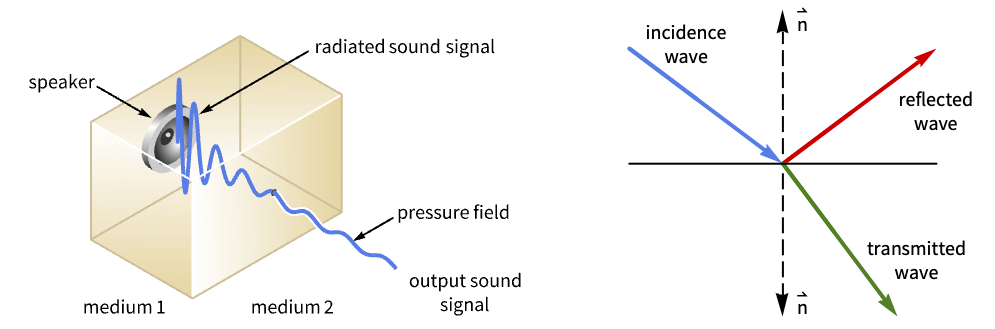
- AcousticImpedanceValue 通常用于模拟对声音部分透明的边界材料.
- AcousticImpedanceValue 模拟时域或频域阻抗,其中因变量压强
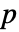 (单位为
(单位为 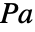 ),自变量
),自变量 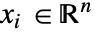 (单位为
(单位为 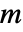 ),时间变量
),时间变量 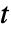 (单位为
(单位为 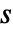 ),或频率变量
),或频率变量 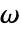 (单位为
(单位为 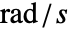 ).
). - 与时间相关的变量 vars 为 vars={p[t,x1,…,xn],t,{x1,…,xn}}.
- 与频率相关的变量 vars 为 vars={p[x1,…,xn],ω,{x1,…,xn}}.
- 时域声学模型 AcousticPDEComponent 基于如下波动方程,其中时间变量为
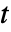 ,密度为
,密度为 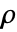 ,声速为
,声速为 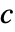 ,声源为
,声源为 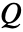 和
和 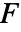 :
: - 频域声学模型 AcousticPDEComponent 基于角频率为
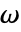 的亥姆霍兹方程:
的亥姆霍兹方程: - 时域阻抗值 AcousticImpedanceValue 模型,其中阻抗为
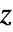 (单位为
(单位为 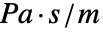 ),边界单位法线为
),边界单位法线为 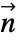 :
: - 频域阻抗值 AcousticImpedanceValue 模型:
- 模型参数 pars 与 AcousticPDEComponent 所指定的相同.
- 可以给出以下模型参数 pars:
-
参数 缺省值 符号 "SpecificAcousticImpedance" Infinity 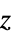 ,声阻抗,单位为
,声阻抗,单位为 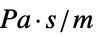
- AcousticImpedanceValue 运算为广义 NeumannValue.
- 边界谓词 pred 可以像在 NeumannValue 中一样指定.
- 阻抗边界可用于以下场合:
-
分析类型 是否适用 时域 是 频域 是 本征频率 否 - 如果 AcousticImpedanceValue 取决于在关联 pars 中指定为 …,keypi…,pivi,…] 的参数
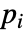 ,则参数
,则参数 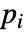 用
用 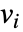 代替.
代替.
范例
打开所有单元关闭所有单元基本范例 (5)
应用 (1)
下面的声学模型描述了一个开放式管道,在管道的一端放置了一个振动活塞,而管道的另一端则通向一个无限域. 在这种情况下,在一端设置一个阻抗边界条件来模拟无限域. 要模拟的管道是一个法兰圆管,如下图所示:
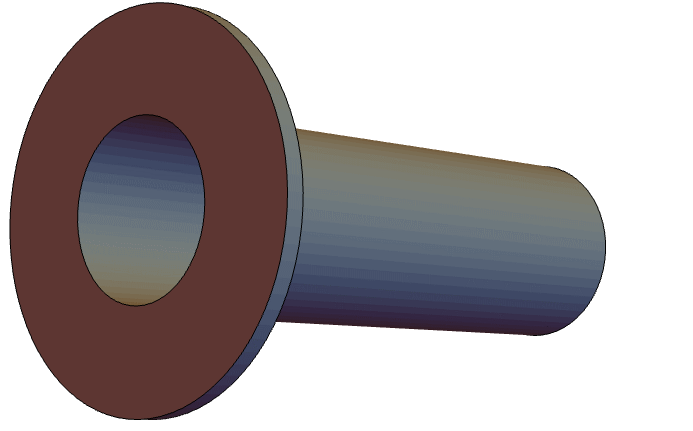
由于管道的几何形状和边界条件关于 ![]() 轴是旋转对称的,因此可以使用轴对称模型. 描述声波传播的指导方程是轴对称亥姆霍兹 (Helmholtz) 方程.
轴是旋转对称的,因此可以使用轴对称模型. 描述声波传播的指导方程是轴对称亥姆霍兹 (Helmholtz) 方程.
轴对称几何体可以用一个二维矩形近似表示,该矩形代表管道在 ![]() 平面上的横截面:
平面上的横截面:
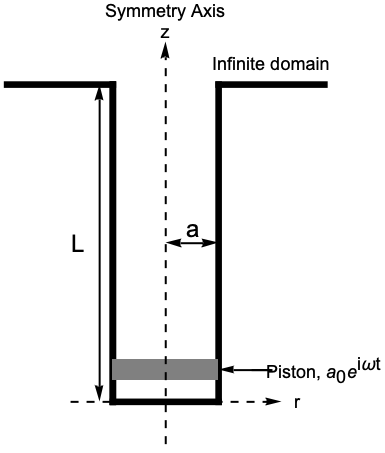
在模型中,有两个边界条件. 一个是 NeumannValue ,表示活塞的加速度 ![]() ,其中
,其中 ![]() :
:
第二个边界条件是具有阻抗 ![]() 的 AcousticImpedanceValue. 阻抗
的 AcousticImpedanceValue. 阻抗 ![]() 由以下近似值给出,其中
由以下近似值给出,其中 ![]() 是波数:
是波数:
用 ![]() 求解 PDE,其中 MaxCellMeasure 由
求解 PDE,其中 MaxCellMeasure 由 ![]() 定义,分辨率为 12,以获得精确结果:
定义,分辨率为 12,以获得精确结果:
可能存在的问题 (1)
"SpecificAcousticImpedance" 的缺省值为 Infinity:
文本
Wolfram Research (2020),AcousticImpedanceValue,Wolfram 语言函数,https://reference.wolfram.com/language/ref/AcousticImpedanceValue.html.
CMS
Wolfram 语言. 2020. "AcousticImpedanceValue." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/AcousticImpedanceValue.html.
APA
Wolfram 语言. (2020). AcousticImpedanceValue. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AcousticImpedanceValue.html 年