AntihermitianMatrixQ
更多信息和选项

- AntihermitianMatrixQ 也被称为斜埃尔米特矩阵.
- 如果 m-ConjugateTranspose[m],则矩阵 m 为反埃尔米特矩阵.
- AntihermitianMatrixQ 适用于符号和数值矩阵.
- 可以给出下列选项:
-
SameTest Automatic 检验表达式相等性的函数 Tolerance Automatic 数值近似的偏差 - 对于精确和符号矩阵,如果 f[mij,mkl] 给出 True,选项 SameTest->f 表示 mij 和 mkl 这两个项相等.
- 对于近似矩阵,可以使用选项 Tolerance->t 表示所有的项 Abs[mij]≤t 均为零.
- 对于矩阵的项 Abs[mij]>t,都进行相等性比较,除最后一个
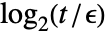 位外,其中对于 MachinePrecision 矩阵,
位外,其中对于 MachinePrecision 矩阵,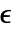 为 $MachineEpsilon,对于 Precision 为
为 $MachineEpsilon,对于 Precision 为 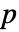 的矩阵,
的矩阵,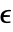 为
为 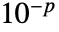 .
.
范例
打开所有单元关闭所有单元范围 (10)
基础用法 (6)
将 AntihermitianMatrixQ 用于任意精度矩阵:
将 AntihermitianMatrixQ 用于符号矩阵:
当 c=-b 且 a 和 d 的实部为零时,该矩阵变为反埃尔米特矩阵:
AntihermitianMatrixQ 可高效地处理大型数值矩阵:
特殊矩阵 (4)
将 AntihermitianMatrixQ 用于稀疏矩阵:
将 AntihermitianMatrixQ 用于结构化矩阵:
用于 QuantityArray 结构化矩阵:
HilbertMatrix 不是反埃尔米特矩阵:
选项 (2)
SameTest (1)
对于正实数 ![]() ,矩阵为反埃尔米特矩阵,但 AntihermitianMatrixQ 给出 False:
,矩阵为反埃尔米特矩阵,但 AntihermitianMatrixQ 给出 False:
使用选项 SameTest 得到正确的答案:
Tolerance (1)
应用 (6)
使用 Table 生成反埃尔米特矩阵:
SymmetrizedArray 可以生成具有对称性的矩阵(和一般数组):
使用 Normal 转换回普通矩阵:
斯通定理阐述,任何单参数的酉矩阵系列都有一个反埃尔米特对数导数. 验证以下矩阵系列的定理:
在量子力学中,时间演化由酉矩阵的单参数系列 ![]() 表示.
表示. ![]() 乘以
乘以 ![]() 的对数导数是称为哈密顿量或能量算子
的对数导数是称为哈密顿量或能量算子 ![]() 的埃尔米特矩阵. 其特征值代表系统的可能能量. 对于以下时间演化,计算哈密顿量和可能的能量:
的埃尔米特矩阵. 其特征值代表系统的可能能量. 对于以下时间演化,计算哈密顿量和可能的能量:
反埃尔米特矩阵 ![]() 的 MatrixExp[v] 是酉矩阵. 通过其微分方程
的 MatrixExp[v] 是酉矩阵. 通过其微分方程 ![]() 定义矩阵函数,其中初始值为
定义矩阵函数,其中初始值为 ![]() ,表明解是酉型的:
,表明解是酉型的:
属性和关系 (15)
对于任何不是矩阵的 x,AntihermitianMatrixQ[x] 都会返回 False:
如果 m==-ConjugateTranspose[m],则矩阵为反埃尔米特矩阵:
使用 Diagonal 可选出对角线元素:
使用 Symmetrize 和对称 Antihermitian 来计算矩阵的反埃尔米特部分:
这等于 m 和 ConjugateTranspose[m] 之间的归一化差:
使用 HermitianMatrixQ 检验矩阵是否是埃尔米特矩阵:
反埃尔米特矩阵 m 的 MatrixExp[m] 是酉矩阵:
使用 NormalMatrixQ 检验矩阵是否为正规矩阵:
使用 Eigenvalues 求特征值:
反埃尔米特矩阵 m 的 CharacteristicPolynomial[m,x] 交替实部和虚部系数:
使用 Eigenvectors 求特征向量:
奇数维反对称矩阵 m 的 Det[m] 是虚数:
文本
Wolfram Research (2014),AntihermitianMatrixQ,Wolfram 语言函数,https://reference.wolfram.com/language/ref/AntihermitianMatrixQ.html.
CMS
Wolfram 语言. 2014. "AntihermitianMatrixQ." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/AntihermitianMatrixQ.html.
APA
Wolfram 语言. (2014). AntihermitianMatrixQ. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AntihermitianMatrixQ.html 年