AudioBlockMap[f,audio,dur]
applies f to non-overlapping partitions of length dur in audio.
AudioBlockMap[f,audio,{dur,offset}]
applies f to partitions with offset offset in audio.
AudioBlockMap[f,audio,{dur,offset,wfun}]
applies f after applying wfun to partitions in audio.


AudioBlockMap
AudioBlockMap[f,audio,dur]
applies f to non-overlapping partitions of length dur in audio.
AudioBlockMap[f,audio,{dur,offset}]
applies f to partitions with offset offset in audio.
AudioBlockMap[f,audio,{dur,offset,wfun}]
applies f after applying wfun to partitions in audio.
Details and Options



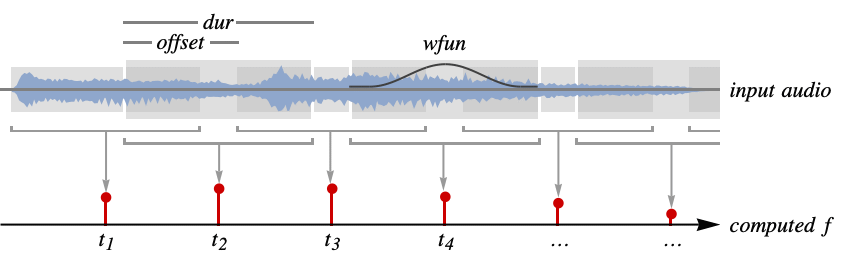
- AudioBlockMap[f,audio,…] returns a TimeSeries whose values are the results of f applied to the partitions of audio. The times are the centers of the corresponding partitions.
- Function f can work on different forms of the partition data using named arguments:
-
#AudioData or #1 raw audio data of each partition (default) #FourierData Fourier transform of each partition #MagnitudeSpectrum magnitude of the Fourier transform #PowerSpectrum power spectrum of each partition - Time variables dur and offset can be given as a scalar in seconds, or a time or sample Quantity object.
- The smoothing window wfun can be specified using a window function that will be sampled between
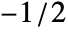 and
and 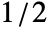 or a list of values resampled to the length of the partition. By default, no smoothing is performed, which is equivalent to DirichletWindow.
or a list of values resampled to the length of the partition. By default, no smoothing is performed, which is equivalent to DirichletWindow. - The following options can be given:
-
Alignment Center alignment of the time stamps with partitions FourierParameters {-1,1} Fourier parameters MetaInformation None include additional metainformation MissingDataMethod None method to use for missing values Padding Automatic padding scheme PaddingSize Automatic amount of padding ResamplingMethod "Interpolation" the method to use for resampling paths - Possible settings for Alignment include:
-
Left return times at the beginning of each partition Center return times at the center of each partition Right return times at the end of each partition a scaled alignment between -1 (left) and 1 (right) - Possible settings for Padding include:
-
None no padding, dropping partitions with fewer samples 0 zero (silence) padding val a constant value "Fixed" repetitions of the boundary value "Periodic" cyclic repetitions of the complete audio "Reflected" reflections of the audio at the boundary "Reversed" reversals of the complete audio
Examples
open all close allBasic Examples (1)
Scope (7)
Function Specification (5)
The function f can return any value supported by TimeSeries:
Compute a pair of minimum and maximum values on each partition:
The function f does not need to return numeric output:
This function returns a color proportional to the maximum value in the partition:
Plot the result alongside the waveform:
The function f can operate on the Fourier transform of the partition data:
Compute the phase of the 100th components of the Fourier transform:
Plot the result alongside the waveform:
The function f can operate on the magnitude spectrum of the partition data:
Find the position of the second biggest peak in the magnitude spectrum:
Plot the result alongside the waveform:
The function f can operate on the power spectrum of the partition data:
Filter each power spectrum with a lowpass filter to smooth the result:
Partition Specification (2)
Compute maximum value of non-overlapping segments of 0.05 seconds:
Plot the result along with the audio waveform:
Use 0.02 seconds of overlap between segments:
Plot the result along with the audio waveform:
Plot the result along with the audio waveform:
The partition size and the offset can be specified as a time Quantity, a "Samples" Quantity, or a number, interpreted as duration in seconds:
Options (2)
Alignment (1)
The time stamps of the resulting TimeSeries are by default placed in the center of each partition:
Center alignment is the same as Alignment->0:
Use Alignment->Right to return the computed property at the end of each partition:
Applications (3)
Compute the instantaneous amplitude in dB RMS:
Visualize the histogram of the instantaneous amplitude in dB RMS:
Use the resulting distribution to perform analysis, including visualizing distribution functions:
Compute the RMS amplitude of the signal with a threshold of 0.02:
Properties & Relations (1)
Many AudioLocalMeasurements properties can be computed using AudioBlockMap:
Interactive Examples (1)
Related Guides
Text
Wolfram Research (2016), AudioBlockMap, Wolfram Language function, https://reference.wolfram.com/language/ref/AudioBlockMap.html (updated 2019).
CMS
Wolfram Language. 2016. "AudioBlockMap." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/AudioBlockMap.html.
APA
Wolfram Language. (2016). AudioBlockMap. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AudioBlockMap.html
BibTeX
@misc{reference.wolfram_2025_audioblockmap, author="Wolfram Research", title="{AudioBlockMap}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/AudioBlockMap.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_audioblockmap, organization={Wolfram Research}, title={AudioBlockMap}, year={2019}, url={https://reference.wolfram.com/language/ref/AudioBlockMap.html}, note=[Accessed: 09-March-2026]}