Circumsphere
Circumsphere[{p1,…,pn+1}]
![]() 内の点 piに外接する球を返す.
内の点 piに外接する球を返す.
Circumsphere[poly]
多面体あるいは多角形 poly の外接球を与える.
詳細

- Circumsphereは,外接円としても知られている.
- Circumsphereは,(弧長,面積等が)最小の点 piに外接するSphereを与える.
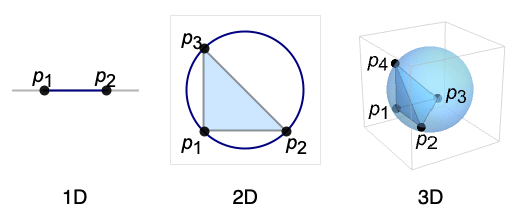
- Circumsphereを評価するとSphere[c,r]になる.中心 c はSimplex[{p1,…,pn+1}]の外心として,半径 r はその外接半径として知られている.
- Circumsphereは
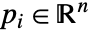 について定義され,アフィン独立である.
について定義され,アフィン独立である. - 多面体については,Circumsphere[poly]はCircumsphere[PolyhedronCoordinates[poly]]に等しい.
- 多角形については,Circumsphere[poly]はCircumsphere[PolygonCoordinates[poly]]に等しい.
- Circumsphereは,GeometricSceneの記号的な点と一緒に使うことができる.
例題
すべて開くすべて閉じるスコープ (17)
グラフィックス (6)
指定 (2)
領域 (11)
Circumsphereは任意数の次元で使うことができる:
Circumsphere上で方程式を解く:
アプリケーション (7)
LineとCircumsphereの交点を求める:
DelaunayMeshの定義特性は,いかなる入力点もメッシュ中の任意のTriangleの外接円中に含まれない,というものである:
Circumsphereを使って関数の曲率の半径を近似する:
Circumsphereを使って,三角形分割されている任意の領域を被覆する円板を求める.まず,領域を三角形分割する:
Circumsphereを使って各三角形についての円を計算する:
Circumsphereを使って,三角形分割された領域を被覆する球体を生成する.まず,領域を離散化し,三角形分割する:
Circumsphereを使って各四面体についての球を計算する:
特性と関係 (1)
Circumsphereは,2Dにおける球面上の3点を拾うことで,任意のSphereを表すことができる:
テキスト
Wolfram Research (2014), Circumsphere, Wolfram言語関数, https://reference.wolfram.com/language/ref/Circumsphere.html (2019年に更新).
CMS
Wolfram Language. 2014. "Circumsphere." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Circumsphere.html.
APA
Wolfram Language. (2014). Circumsphere. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Circumsphere.html