ContinuousWaveletData

ContinuousWaveletData[{{oct1,voc1}coef1,…},wave]

产生一个连续小波数据对象，其中小波系数为对应于倍频程与音频 {octi,voci} 的 coefi，小波为 wave.

更多信息和选项

  • ContinuousWaveletData[{{oct1,voc1}->coef1,…},…] 恒能转换为结构为 ContinuousWaveletData[coefs,octvocs,…] 的最佳标准形式.
  • 系数 coefi 可以为向量、 Sound[…] 或 SampledSoundList[…]对象.
  • ContinuousWaveletTransform 所用的选项也可用作 ContinuousWaveletData 的选项.
  • 在标准输出形式中，仅打印原始数据的倍频程数、音频数与维数.
  • Normal[ContinuousWaveletData[…]] 给出规则列表 {{oct1,voc1}->coef1,{oct2,voc2}->coef2,…}，该规则列表给出每一对倍频程与音频 {octi,voci} 和对应的系数数组 coefi 的对应关系.
  • ContinuousWaveletData 表示多重尺度 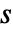上的连续小波变换 w(u,s)=1/(sqrt(s))sum_(k=1)^nx_k TemplateBox[{psi}, Conjugate]((Delta (k-u))/s).
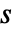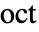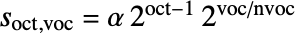  • 各尺度 由一个倍频程数 与音频数 指定，并由 得到.
  • 尺度 {oct,voc} 可用于从 ContinuousWaveletData 对象 cwd 中提取小波系数. 可以给出下列指定：
  • cwd[{oct,voc}]提取对应于 {oct,voc} 的系数
    cwd[{{oct1,voc1},{oct2,voc2},…}]提取多个小波系数数组
    cwd[ovpatt]提取尺度匹配 ovpatt 的全部系数
    cwd[All]提取全部系数
  • 缺省时，系数以规则列表 {{oct1,voc1}->coef1,{oct2,voc2}->coef2,…} 的形式返回.
  • cwd[…,{form1,form2,…}] 可用于控制输出形式. 可能的形式 formi 包括：
  • "Rules"规则 {{oct1,voc1}->…}
    "Values"仅系数
    "Inverse"个别系数的逆变换
    "ListPlot"1D 系数的简单列表图形
    "Sound"声音系数的声音对象
    "SampledSoundList"声音系数的取样声音对象
  • 小波表示的属性由 ContinuousWaveletData[…]["prop"] 得到.
  • ContinuousWaveletData[…]["Properties"] 给出 ContinuousWaveletData 对象可用的属性列表.
  • 与变换系数相关的属性包括：
  • "Octaves"所用的倍频程数
    "Voices"每个倍频程所用的音频数
    "Scales"所用的小波尺度
    "Wavelet"所用的小波族
    "WaveletScale"最小的可解尺度
    "WaveletIndex"全部小波索引{octi,voci}的列表
    "LogScalogramFunction"给出函数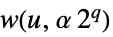
    "LinearScalogramFunction"给出函数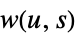
  • 与输入数据相关的属性包括：
  • "DataDimensions"原始数据的维数
    "DataChannels"数据的频道数
    "DataMean"原始数据的均值
    "DataWrapper"在重构后应用于数据的封装函数
    "SampleRate"用于输入数据的样本率

范例

打开所有单元关闭所有单元

基本范例  (2)

得到 ContinuousWaveletData 对象：

ContinuousWaveletData 表示不同尺度 {oct,voc} 上的系数数组：

提取包括对应于各 {oct,voc} 的数值尺度在内的属性：

计算任意连续小波变换系数小波逆变换：

范围  (12)

基本用途  (10)

由 ContinuousWaveletTransform 得到一个 ContinuousWaveletData 对象：

显示计算尺度 {oct,voc} 的列表：

得到作为规则列表的系数数组：

InverseContinuousWaveletTransform 在 ContinuousWaveletData 上运算：

在足够的倍频程与音频的条件下，逆变换给出准确的重构：

提取对应于具体倍频程与音频的系数：

提取一个单一系数数组：

利用模式 {1,_} 提取第一个倍频程的全部系数：

指定包括指定 {oct,voc} 与模式的列表：

得到不同形式的系数数组：

得到一个规则列表（缺省）：

仅得到值：

得到作为小列表图的系数：

得到每个系数数组的逆变换：

组合形式：

得到作为 Sound 对象的声音小波系数：

提取小波变换数据的属性：

倍频程数、音频数，及所用的小波：

所有可用属性：

在其它小波函数中使用 ContinuousWaveletData：

逆变换：

尺度谱图：

变换 ContinuousWaveletData：

对各系数应用任意函数：

将所有与指定 {oct,voc} 匹配的系数设置为零：

比较尺度谱图：

由一个给出系数数组的规则列表构造 ContinuousWaveletData：

结果表示一个包括指定系数在内的倍频程和音频范围：

其它系数假定为零：

构造一个使用指定小波的 ContinuousWaveletData：

指定的小波用于逆变换：

属性  (2)

得到连续小波变换的属性：

所用的小波与小波尺度：

变换系数的属性，包括倍频程数与音频数：

所有可用 {oct,voc} 的列表：

对应于各 {oct,voc} 的数值尺度：

与输入数据相关的属性：

数据维数、声频通道数以及样本率：

自动应用于逆变换结果的封装函数：

选项  (5)

SampleRate  (1)

对于 Sound 输入，自动计算 SampleRate：

默认情况下，从第一个系数规则提取 SampleRate：

显式指定 SampleRate：

WaveletScale  (2)

默认情况下，自动计算 WaveletScale：

设置 ContinuousWaveletData：

显式设置 WaveletScale：

WorkingPrecision  (2)

默认情况下，使用 WorkingPrecision->MachinePrecision：

使用较高精度的计算：

在数值接近零的情况下，准确度是正确数位数目的较好的指示：

属性和关系  (5)

各小波系数数组的长度等于数据的长度：

ContinuousWaveletData 表示在一组尺度上的连续变换系数：

DiscreteWaveletData 表示一个离散变换系数的树结构：

从系数和属性重建一个 ContinuousWaveletData：

指定所使用的系数和小波：

数据维度从系数确定：

比较逆变换：

得到作为规则列表的全部系数的其它方式：

使用 Normal：

显式提取 All 系数：

指定模式 Blank[] (_)，匹配任何倍频程与音频：

仅得到系数列表的等价方式：

将 Last 应用于各个由 cwd[{oct,voc}] 返回的规则：

使用 Part：

显式仅得到系数值：

Wolfram Research (2010)，ContinuousWaveletData，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ContinuousWaveletData.html.

文本

Wolfram Research (2010)，ContinuousWaveletData，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ContinuousWaveletData.html.

CMS

Wolfram 语言. 2010. "ContinuousWaveletData." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ContinuousWaveletData.html.

APA

Wolfram 语言. (2010). ContinuousWaveletData. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ContinuousWaveletData.html 年

BibTeX

@misc{reference.wolfram_2024_continuouswaveletdata, author="Wolfram Research", title="{ContinuousWaveletData}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/ContinuousWaveletData.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_continuouswaveletdata, organization={Wolfram Research}, title={ContinuousWaveletData}, year={2010}, url={https://reference.wolfram.com/language/ref/ContinuousWaveletData.html}, note=[Accessed: 05-November-2024 ]}