ContinuousWaveletTransform

ContinuousWaveletTransform[{x₁,x₂,…}]

値 x_iのリストの連続ウェーブレット変換を与える．

ContinuousWaveletTransform[data,wave]

ウェーブレット wave を使った連続ウェーブレット変換を与える．

ContinuousWaveletTransform[data,wave,{noct,nvoc}]

1オクターブにつき nvoc 音のオクターブを noct 個を使った連続ウェーブレット変換を与える．

ContinuousWaveletTransform[sound,…]

サンプルサウンドの連続ウェーブレット変換を与える．

詳細とオプション

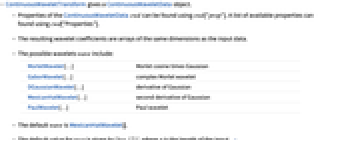
ContinuousWaveletTransformはContinuousWaveletDataオブジェクトを与える．
ContinuousWaveletData cwd の特性は cwd["prop"]で得ることができる．使用可能な特性のリストは cwd["Properties"]で得られる．
結果のウェーブレット係数は入力データと同じ次元の配列である．
使用可能なウェーブレット wave

	MorletWavelet[…]	Morletコサイン x ガウスウェーブレット
	GaborWavelet[…]	複素Morletウェーブレット
	DGaussianWavelet[…]	ガウスウェーブレットの導関数
	MexicanHatWavelet[…]	ガウスウェーブレットの二次導関数
	PaulWavelet[…]	Paulウェーブレット

デフォルトの wave はMexicanHatWavelet[]である．
noct のデフォルト値は $TemplateBox[{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, {n, /, 2}, )}}, Floor]$ で与えられる．ただし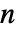，は入力の長さである． »
nvoc のデフォルト値は4である．
関数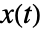の連続ウェーブレット変換は $w(u,s)=1/(sqrt(s))int_(-infty)^inftyx(t) TemplateBox[{psi}, Conjugate]((t-u)/s)dt$ で与えられる．
一様にサンプルされた数列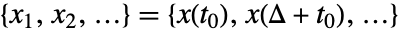の連続ウェーブレット変換は $w(u,s)=1/(sqrt(s))sum_(k=1)^nx_k TemplateBox[{psi}, Conjugate]((Delta (k-u))/s)$ で与えられる．
スケーリングパラメータ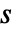は均等に調律されたスケール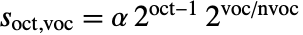で与えられる．ただし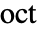，はオクターブの数，は音の数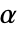，は最小ウェーブレットスケールである．
各スケール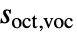につき，ContinuousWaveletTransformはウェーブレット係数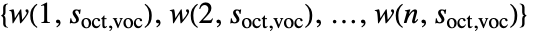を計算する．
使用可能なオプション

Padding	None	データを境界範囲外にどのように延長するか
SampleRate	Automatic	単位あたりのサンプル
WaveletScale	Automatic	分割可能な最小スケール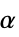
WorkingPrecision	MachinePrecision	内部計算で使用する精度

Paddingは入力 data を次に大きい2のベキ乗まで充填して境界効果を減少させる．Paddingの設定値はArrayPadで使われる充填引数のそれに等しい．
InverseContinuousWaveletTransformは逆変換を行う．

例題

すべて開くすべて閉じる

例 (2)

MexicanHatWaveletを使って連続ウェーブレット変換を計算する：

係数をプロットする：

逆連続ウェーブレット変換を行う：

サンプルのSoundオブジェクトを変換する：

スケログラムをプロットする：

スコープ (18)

基本的な用法 (6)

連続ウェーブレット変換を計算する：

第8オクターブのすべての音を示す：

Normalを使ってすべてのウェーブレット係数を明示的に得る：

Allを引数として使ってすべての係数を得る：

"IndexMap"を使ってどのウェーブレット係数が使えるかを見る：

特定の係数配列を抽出する：

ウェーブレット指標指定のリストに対応するいくつかの係数配列を抽出する：

ウェーブレット指標がパターンにマッチするすべての係数を抽出する：

WaveletScalogramはウェーブレット係数のタイムスケール表現を与える：

オクターブ中の音を多くするとスケールの解像度が増す：

オクターブの数が大きくなるとスケール範囲のスペクトルが広くなる：

タイムとスケールの特徴 (4)

同じスケールの水平帯として単調が現れる：

同じスケールで多重周波数が複数帯として現れる：

線形に周波数が増す正弦曲線：

ウェーブレット変換は特徴をうまく時間で局所化する：

高い周波数は低いオクターブで分解され，低い周波数は高いオクターブで分解される：

信号の時間と周波数の特徴を分解する：

GaborWaveletを使って連続ウェーブレット変換を行う：

スケールの値と周波数の値は反比例する：

周波数を20Hzと70Hzに分解する{oct,voc}ペアを求める：

WaveletScalogramを使って確認する：

ウェーブレット族 (6)

さまざまなウェーブレット族を使ってウェーブレット変換を計算する：

狭いウェーブレット関数を使うと時間とスケールの分解がうまくいく：

広いウェーブレット関数では時間とスケールの分解がうまくいかない：

ウェーブレットの別の族を使って別の特徴を捉える：

MexicanHatWavelet（デフォルト）：

DGaussianWavelet：

GaborWavelet：

MorletWavelet：

PaulWavelet：

サウンド (2)

ContinuousWaveletTransformは入力としてのSoundに使うことができる：

ContinuousWaveletTransformを使った音声分析：

オレンジ色の部分は「You will return safely to Earth」の単語に対応する：

オクターブ5と6を抽出する：

オプション (9)

Padding (3)

Paddingの設定値はArrayPadのメソッドのものと同じで"Periodic"を含む：

"Reversed"：

"ReversedNegation"：

"Reflected"：

"ReflectedDifferences"：

"ReversedDifferences"：

"Extrapolated"：

Paddingはウェーブレット係数の長さには影響しない：

Paddingは入力データを次に大きい2のベキ乗まで充填して境界効果を弱める：

始点の境界効果：

終点の境界効果：

SampleRate (3)

リストの場合，SampleRateのAutomaticの値は1に設定されている：

サンプルレートを明示的に設定する：

Soundデータの場合は，SampleRateのAutomaticの値はSoundデータオブジェクトから抽出される：

SampleRateを使ってウェーブレット変換係数が正規化される：

WaveletScale (1)

WaveletScaleは変換に使われる最小の分解可能スケールを示す：

使われるスケールはで与えられる．はウェーブレットスケール，はオクターブ，は音である：

WorkingPrecision (2)

デフォルトでWorkingPrecision->MachinePrecisionが使われる：

より精度の高い計算を使う：

アプリケーション (4)

同一性の特徴 (2)

実際のウェーブレット関数を使って峰や不連続箇所を分離することができる：

複素ウェーブレットを使って振動運動を捉えることができる：

ウェーブレット係数の振幅：

ウェーブレット係数の位相：

周波数のフィルタ (2)

ContinuousWaveletTransformを使って周波数をフィルタすることができる：

周波数のコサイン波をフィルタする：

InverseContinuousWaveletTransformを閾値データオブジェクトに対して実行する：

フィルタされた最終信号：

スカログラムを使って音符を同定する：

300Hzに相当する平均律に調律された一連のピッチ生成する：

オクターブと音に相当する分解された周波数を計算する：

周波数を300Hzに分解する{oct,voc}ペアを求める：

特性と関係 (1)

オクターブのデフォルト値は $TemplateBox[{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, {n, /, 2}, )}}, Floor]$ で与えられる：

音のデフォルト値は4である：

考えられる問題 (1)

低周波数データは高オクターブで分解される：

入力データの長さに基づき，オクターブのAutomatic設定は8オクターブで分解する：

オクターブの数を増して低周波数要素を分解する：

おもしろい例題 (1)

Zeta関数のスカログラム：

トップへ