ContinuousWaveletTransform
ContinuousWaveletTransform[{x1,x2,…}]
给出一列 xi 值的连续小波变换.
ContinuousWaveletTransform[data,wave]
给出使用小波 wave 的连续小波变换.
ContinuousWaveletTransform[data,wave,{noct,nvoc}]
给出连续小波变换,其中倍频程为使用 noct,每个倍频程的音频数为 nvoc.
ContinuousWaveletTransform[sound,…]
给出声音样本的连续小波变换.
更多信息和选项
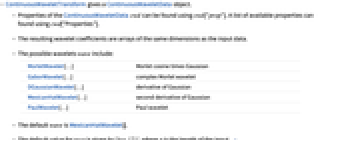

- ContinuousWaveletTransform 给出一个 ContinuousWaveletData 对象.
- ContinuousWaveletData 的 属性 cwd 可以使用 cwd["prop"] 得到. 使用 cwd["Properties"] 可以得到一个可用属性的列表.
- 得到的小波系数是与输入数据具有相同维数的数组.
- 可能的小波 wave 包括:
-
MorletWavelet[…] Morlet 余弦乘以 Gaussian GaborWavelet[…] 复数 Morlet 小波 DGaussianWavelet[…] 高斯导数 MexicanHatWavelet[…] 二阶高斯导数 PaulWavelet[…] Paul 小波 - 缺省的 wave 为 MexicanHatWavelet[].
- noct 的缺省值由
![TemplateBox[{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, {n, /, 2}, )}}, Floor] TemplateBox[{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, {n, /, 2}, )}}, Floor]](Files/ContinuousWaveletTransform.zh/1.png) 得到,其中
得到,其中 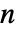 为输入的长度. »
为输入的长度. » - nvoc 的缺省值为 4.
- 函数
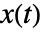 的连续小波变换由
的连续小波变换由 /s)dt w(u,s)=1/(sqrt(s))int_(-infty)^inftyx(t) TemplateBox[{psi}, Conjugate]((t-u)/s)dt](Files/ContinuousWaveletTransform.zh/4.png) 得到.
得到. - 均匀采样序列
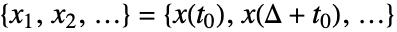 的连续小波变换由
的连续小波变换由 )/s) w(u,s)=1/(sqrt(s))sum_(k=1)^nx_k TemplateBox[{psi}, Conjugate]((Delta (k-u))/s)](Files/ContinuousWaveletTransform.zh/6.png) 得到.
得到. - 尺度参数
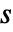 由等调和尺度
由等调和尺度 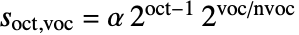 给出,其中
给出,其中 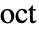 为倍频程数,
为倍频程数, 为音频数,
为音频数,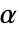 为最小的小波尺度.
为最小的小波尺度. - 对于每个尺度
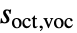 ,ContinuousWaveletTransform 计算小波系数
,ContinuousWaveletTransform 计算小波系数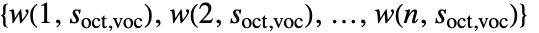 .
. - 可以给出下列选项:
-
Padding None 如何将数据扩展至边界外 SampleRate Automatic 每个单位上的样本 WaveletScale Automatic 最小的可解析尺度 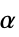
WorkingPrecision MachinePrecision 内部计算所用精度 - Padding 将输入 data 填充至2的第二高次幂以降低边界效应. Padding 的设置与 ArrayPad 中所用的填充参数相同.
- InverseContinuousWaveletTransform 给出逆变换.
范例
打开所有单元关闭所有单元基本范例 (2)
范围 (18)
基本用途 (6)
时间和尺度功能 (4)
较高阶频率在较低倍频程上被解析;较低阶频率在较高倍频程上被解析:
使用 GaborWavelet 进行连续小波变换:
得到解析20到70 赫兹之间频率的数对 {oct,voc}:
利用 WaveletScalogram 验证:
小波族 (6)
MexicanHatWavelet(缺省):
声音 (2)
ContinuousWaveletTransform 作为输入作用于 Sound:
利用 ContinuousWaveletTransform 进行语音分析:
选项 (9)
Padding (3)
WaveletScale (3)
SampleRate (1)
对于列表,SampleRate 的 Automatic 值设为1:
对于 Sound 数据,SampleRate 的 Automatic 值从 Sound 数据对象中提取:
SampleRate 用于小波变换系数的标准化:
WorkingPrecision (2)
应用 (4)
滤波器频率 (2)
ContinuousWaveletTransform 可用于滤波频率:
关于一个阈值数据对象进行 InverseContinuousWaveletTransform:
可能存在的问题 (1)
巧妙范例 (1)
Zeta 函数的尺度谱图:
文本
Wolfram Research (2010),ContinuousWaveletTransform,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ContinuousWaveletTransform.html.
CMS
Wolfram 语言. 2010. "ContinuousWaveletTransform." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ContinuousWaveletTransform.html.
APA
Wolfram 语言. (2010). ContinuousWaveletTransform. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ContinuousWaveletTransform.html 年