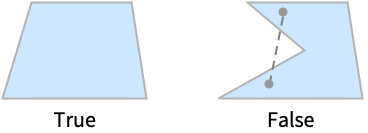
Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

ConvexPolygonQ

ConvexPolygonQ[poly]

如果 poly 是凸多边形，就给出 True，否则给出 False.

更多信息

如果多边形中两个点之间的线段都没有超出多边形，则该多边形为凸多边形.

凸多边形从多边形中的所有点都可见.

范例

打开所有单元关闭所有单元

基本范例 (2)

测试一个多边形是否是凸多边形：

对于非凸多边形，ConvexPolygonQ 给出 False：

范围 (7)

ConvexPolygonQ 适用于多边形：

三角形：

长方形：

有洞的多边形：

自相交多边形：

有不相连组件的多边形：

中的多边形：

ConvexPolygonQ 适用于地理实体的多边形：

具有 GeoPosition 的多边形：

具有 GeoPositionXYZ 的多边形：

具有 GeoPositionENU 的多边形：

ConvexPolygonQ 用于具有 GeoGridPosition 的多边形：

应用 (4)

生成随机多边形以测试算法和验证时间复杂度：

凸多边形算法的时间复杂度：

测试多边形是否是凹多边形：

尝试测试几何区域是否是凸域：

使用机器学习进行多边形分类. 在多边形实例上训练分类函数：

用分类函数对新的多边形进行分类：

简单多边形：

星形多边形：

属性和关系 (6)

凸多边形是简单多边形：

凸多边形的 OuterPolygon 还是凸多边形：

凸多边形没有内多边形：

凸多边形的所有内角都小于：

用 PolygonDecomposition 将多边形分解为凸多边形：

用 RandomPolygon 生成凸多边形：

凸多边形是其边组成的凸包：

可能存在的问题 (1)

对于非恒定多边形，ConvexPolygonQ 返回 False：

顶部