DifferentiatorFilter

DifferentiatorFilter[data,ωc]

applies a differentiator filter with a cutoff frequency ωc to an array of data.

DifferentiatorFilter[data,ωc,n]

uses a filter kernel of length n.

DifferentiatorFilter[data,ωc,n,wfun]

applies a smoothing window wfun to the filter kernel.

Details and Options

  • DifferentiatorFilter is a finite impulse response (FIR) discrete-time filter that is commonly used to approximate the derivative of sampled data.
  • The data can be any of the following:
  • listarbitrary-rank numerical array
    tseriestemporal data such as TimeSeries and TemporalData
    imagearbitrary Image or Image3D object
    audioan Audio or Sound object
  • When applied to images and multidimensional arrays, filtering is applied successively to each dimension, starting at level 1. DifferentiatorFilter[data,{ωc1,ωc2,…}] uses the frequency ωci for the i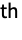^(th) dimension.
  • Filtering with cutoff frequency ωc reduces the susceptibility of the derivative to signal noise, with the amount of smoothing dependent on the value of the cutoff frequency ωc.
  • The cutoff frequency ωc should be between 0 and 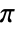. Smaller values of ωc result in greater smoothing.
  • DifferentiatorFilter[data,ωc] uses a filter kernel length and smoothing window suitable for the cutoff frequency ωc and the input data.
  • Typical smoothing windows wfun include:
  • BlackmanWindowsmoothing with a Blackman window
    DirichletWindowno smoothing
    HammingWindowsmoothing with a Hamming window
    {v1,v2,…}use a window with values vi
    fcreate a window by sampling f between 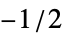and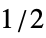
  • The following options can be given:
  • Padding "Fixed"the padding value to use
    SampleRate Automaticsample rate assumed for the input
  • By default, SampleRate->1 is assumed for images as well as data. For sampled sound objects with sample rate r, SampleRate->r is used.
  • With SampleRate->r, the cutoff frequency ωc should be between 0 and r×.

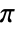Examples

open allclose all

Basic Examples  (2)

Differentiate a sampled cosine signal:

Differentiate an image:

Scope  (9)

Data  (6)

Filter a 1D triangular sequence:

Filter a 2D pulse sequence:

Filter a TimeSeries:

Digital differentiation of a square wave audio signal:

Differentiation of a 3D image:

Filter using exact precision:

Parameters  (3)

With an audio signal, a numeric cutoff frequency is interpreted as radians per second:

Differentiation of a unit step sequence using a filter of length 7:

Use a different cutoff frequency:

Use a specific window function:

Specify the window function as a numeric list:

Use different cutoff frequencies in each dimension:

Options  (4)

Padding  (2)

By default, "Fixed" padding is used:

Use Padding->None to eliminate potential image border artifacts:

Different padding methods result in different edge effects:

SampleRate  (2)

Use a half-band differentiating filter, assuming a normalized sample rate of 1:

Assume a sample rate of 3:

Apply a half-band differentiator filter to audio sampled at a rate of :

Applications  (2)

Use a derivative filter to highlight edges in an image:

Convert a triangle wave to a square wave:

Properties & Relations  (7)

Create a differentiator filter using LeastSquaresFilterKernel and a Hamming window:

Compare with the result of DifferentiatorFilter:

Impulse response of an odd-length, full-band derivative filter of length 21:

Magnitude spectrum of the filter:

Magnitude spectrum of an odd-length, full-band derivative filter with no smoothing window:

Impulse response of an even-length derivative filter:

Magnitude spectrum of the filter:

Magnitude spectrum of an even-length, full-band derivative filter with no smoothing window:

Magnitude response of an odd-length differentiator filter for different filter lengths:

Impulse response of a half-band, odd-length derivative filter:

Magnitude spectrum of the filter:

Possible Issues  (1)

With PaddingNone, the output will be shorter than the input:

Wolfram Research (2012), DifferentiatorFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/DifferentiatorFilter.html (updated 2016).

Text

Wolfram Research (2012), DifferentiatorFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/DifferentiatorFilter.html (updated 2016).

CMS

Wolfram Language. 2012. "DifferentiatorFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/DifferentiatorFilter.html.

APA

Wolfram Language. (2012). DifferentiatorFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DifferentiatorFilter.html

BibTeX

@misc{reference.wolfram_2024_differentiatorfilter, author="Wolfram Research", title="{DifferentiatorFilter}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/DifferentiatorFilter.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_differentiatorfilter, organization={Wolfram Research}, title={DifferentiatorFilter}, year={2016}, url={https://reference.wolfram.com/language/ref/DifferentiatorFilter.html}, note=[Accessed: 22-December-2024 ]}