DifferentiatorFilter

DifferentiatorFilter[data,ωc]

カットオフ周波数 ωcの微分器フィルタをデータ配列に適用する．

DifferentiatorFilter[data,ωc,n]

長さ n のフィルタカーネルを使う．

DifferentiatorFilter[data,ωc,n,wfun]

平滑化窓 wfun をフィルタカーネルに適用する．

詳細とオプション

  • DifferentiatorFilterは，一般にサンプルとして取ったデータの微分の近似に使われる，有限インパルス応答（impulse response，FIR）離散時間フィルタである．
  • data は次のいずれでもよい．
  • list任意階数の数値配列
    tseriesTimeSeriesやTemporalDataのような時間データ
    image任意のImageオブジェクトまたはImage3Dオブジェクト
    audioAudioオブジェクトまたはSoundオブジェクト
  • 画像や多次元配列に適用された場合，フィルタリングはレベル1から始めて各次元に連続的に適用される．DifferentiatorFilter[data,{ωc1,ωc2,…}]は i 次元で周波数 ωci を使う．
  • カットオフ周波数 ωcでフィルタをかけると，微分の信号ノイズに対する感受性が低下する．平滑化の量はカットオフ周波数 ωcに依存する．
  • カットオフ周波数 ωcは0から 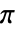まででなければならない．ωcの値が小さいほど滑らかになる．
  • DifferentiatorFilter[data,ωc]はカットオフ周波数 ωcと入力 data に適したフィルタカーネル長と平滑化窓を使う．
  • よく使われる平滑化窓 wfun
  • BlackmanWindowBlackman窓で平滑化する
    DirichletWindow平滑化は行わない
    HammingWindowハミング窓で平滑化する
    {v1,v2,…}値 viの窓を使う
    f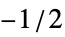から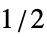の範囲で f をサンプリングすることで窓を作る
  • 使用可能なオプション
  • Padding "Fixed"使用する充填値
    SampleRate Automatic入力に想定されるサンプルレート
  • デフォルトで，データと同様画像にもSampleRate->1が想定される．サンプルレート r のサンプル sound オブジェクトについては，SampleRate->r が使われる．
  • SampleRate->r の場合，カットオフ周波数 ωcは 0から r× 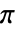まででなければならない．

例題

すべて開くすべて閉じる

例  (2)

サンプルされた余弦信号を微分する：

画像を微分する：

スコープ  (9)

データ  (6)

1D三角列にフィルタをかける：

2Dパルス列にフィルタをかける：

TimeSeriesにフィルタをかける：

矩形波音声信号のデジタル微分：

3D画像の微分：

厳密精度でフィルタをかける：

パラメータ  (3)

音声信号の場合，数値カットオフ周波数はラジアン／秒として解釈される：

長さ7のフィルタを使った単位ステップ列の微分：

別のカットオフ周波数を使う：

特定の窓関数を使う：

窓関数を数値リストとして指定する：

各次元に異なるカットオフ周波数を使う：

オプション  (4)

Padding  (2)

デフォルトで，"Fixed"充填が使われる：

Padding->Noneを使って潜在的な画像境界のアーチファクトを排除する：

充填法を変えるとエッジ効果も変わる：

SampleRate  (2)

正規化されたサンプルレート1を仮定して，ハイバンド微分フィルタを使う：

サンプルレート3を仮定する：

ハイバンド微分器フィルタをレートでサンプルされた音声に適用する：

アプリケーション  (2)

導関数フィルタを使って画像中の辺をハイライトする：

三角波を矩形波に変換する：

特性と関係  (7)

LeastSquaresFilterKernelおよびハミング窓を使って微分器フィルタを作る：

DifferentiatorFilterの結果と比較する：

奇数長，フルバンドで長さ21の導関数フィルタのインパルス応答：

フィルタの振幅スペクトル：

平滑化窓がない，奇数長のフルバンド導関数フィルタの振幅スペクトル：

偶数長のヒルベルトフィルタのインパルス応答：

フィルタの振幅スペクトル：

平滑化窓がない，偶数長のフルバンド導関数フィルタの振幅スペクトル：

平滑化窓がない，奇数長のフルバンドの微分器フィルタの振幅スペクトル：

ハーフバンドで奇数長の導関数フィルタのインパルス応答：

フィルタの振幅スペクトル：

考えられる問題  (1)

PaddingNoneとすると，出力は入力よりも短くなる：

Wolfram Research (2012), DifferentiatorFilter, Wolfram言語関数， https://reference.wolfram.com/language/ref/DifferentiatorFilter.html （2016年に更新）.

テキスト

Wolfram Research (2012), DifferentiatorFilter, Wolfram言語関数， https://reference.wolfram.com/language/ref/DifferentiatorFilter.html （2016年に更新）.

CMS

Wolfram Language. 2012. "DifferentiatorFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/DifferentiatorFilter.html.

APA

Wolfram Language. (2012). DifferentiatorFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DifferentiatorFilter.html

BibTeX

@misc{reference.wolfram_2024_differentiatorfilter, author="Wolfram Research", title="{DifferentiatorFilter}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/DifferentiatorFilter.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_differentiatorfilter, organization={Wolfram Research}, title={DifferentiatorFilter}, year={2016}, url={https://reference.wolfram.com/language/ref/DifferentiatorFilter.html}, note=[Accessed: 22-November-2024 ]}