DifferentiatorFilter

DifferentiatorFilter[data,ωc]

对数据数组应用截止频率为 ωc 的微分滤波器.

DifferentiatorFilter[data,ωc,n]

使用长度为 n 的滤波器核.

DifferentiatorFilter[data,ωc,n,wfun]

对滤波器核应用平滑窗 wfun.

更多信息和选项

  • DifferentiatorFilter 是一个有限冲击响应 (FIR) 离散时间滤波器，通常用于近似采样数据的导数.
  • data 可以采用以下形式：
  • list任意维数的数值数组
    tseries暂态数据，如 TimeSeries 和 TemporalData
    image任意 Image 或 Image3D 对象
    audioAudio 或 Sound 对象
  • 当应用于图像和多维数组时，滤波器连续应用于每个维度，从第 1 层开始. 对第 i 维，DifferentiatorFilter[data,{ωc1,ωc2,…}] 使用频率 ωci.
  • 截止频率为 ωc 的滤波降低了导数对信号噪声的敏感性，平滑量取决于截止频率 ωc 的值.
  • 截止频率 ωc 应位于 0 和 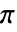之间. ωc 的值越小，平滑度越好.
  • DifferentiatorFilter[data,ωc] 使用适用于截止频率 ωc 和输入 data 的滤波器核长度和平滑窗.
  • 典型的平滑窗 wfun 包括：
  • BlackmanWindow使用 Blackman 窗平滑
    DirichletWindow不使用平滑
    HammingWindow使用 Hamming 窗平滑
    {v1,v2,…}使用值为 vi 的窗
    f通过在 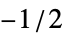和 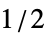之间采样 f 创建窗
  • 可以给出以下选项：
  • Padding "Fixed"要用的填充值
    SampleRate Automatic对输入假定的采样率
  • 默认情况下，对于图像和数据，均有 SampleRate->1. 对于采样率为 r 的采样 sound 对象，使用 SampleRate->r.
  • 当 SampleRate->r 时，截止频率 ωc 应位于 0 和 r× 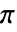之间.

范例

打开所有单元关闭所有单元

基本范例  (2)

对余弦抽样信号进行微分：

对图像求微分：

范围  (9)

数据  (6)

对一维三角序列进行滤波：

对二维脉冲序列进行滤波：

对 TimeSeries 进行滤波：

方波音频信号的数字微分：

三维图像的微分：

精确滤波：

参数  (3)

对于音频信号，数值截止频率会被解释为以弧度每秒为单位：

使用长度为 7 的滤波器对单位阶跃序列进行微分：

使用不同的截止频率：

使用特定窗口函数：

用数值列表指定窗口函数：

在各维度使用不同的截止频率：

选项  (4)

Padding  (2)

缺省情况下，使用 "Fixed" 填充方法：

用 Padding->None 消除潜在的图像边界伪影：

不同的填充方法导致边呈现不同的效果：

SampleRate  (2)

使用微分半带滤波器，假定归一化采样率为 1：

假定采样率为 3：

将微分半带滤波器应用于采样率为 的音频信号：

应用  (2)

使用导数滤波突出显示图像中的边：

将三角波转换为方波：

属性和关系  (7)

使用 LeastSquaresFilterKernel 和 Hamming 窗创建微分滤波器：

与 DifferentiatorFilter 比较：

长度为 21 的全带导数滤波器的冲激响应：

滤波器的幅频响应：

没有平滑窗口的长度为奇数的全带导数滤波器的幅度谱：

长度为偶数的导数滤波器的冲激响应：

滤波器的幅频响应：

没有平滑窗口的长度为偶数的全带导数滤波器的幅度谱：

不同的长度为奇数的微分滤波器的幅值响应：

长度为奇数的半带导数滤波器的冲激响应：

滤波器的幅频响应：

可能存在的问题  (1)

如果设置 PaddingNone，输出的长度将小于输入的长度：

Wolfram Research (2012)，DifferentiatorFilter，Wolfram 语言函数，https://reference.wolfram.com/language/ref/DifferentiatorFilter.html （更新于 2016 年）.

文本

Wolfram Research (2012)，DifferentiatorFilter，Wolfram 语言函数，https://reference.wolfram.com/language/ref/DifferentiatorFilter.html （更新于 2016 年）.

CMS

Wolfram 语言. 2012. "DifferentiatorFilter." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/DifferentiatorFilter.html.

APA

Wolfram 语言. (2012). DifferentiatorFilter. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DifferentiatorFilter.html 年

BibTeX

@misc{reference.wolfram_2024_differentiatorfilter, author="Wolfram Research", title="{DifferentiatorFilter}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/DifferentiatorFilter.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_differentiatorfilter, organization={Wolfram Research}, title={DifferentiatorFilter}, year={2016}, url={https://reference.wolfram.com/language/ref/DifferentiatorFilter.html}, note=[Accessed: 22-November-2024 ]}