WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

DiscreteMaxLimit
✖
DiscreteMaxLimit

✖
DiscreteMaxLimit[f,k∞]

gives the max limit k∞f(k) of the sequence f as k tends to ∞ over the integers.

✖
DiscreteMaxLimit[f,{k1,…,kn}]

gives the nested max limit ⋯ f(k1,…,kn) over the integers.

✖
DiscreteMaxLimit[f,{k1,…,kn}{,…,}]

gives the multivariate max limit f(k1,…,kn) over the integers.

Details and Options

  • DiscreteMaxLimit is also known as limit superior, supremum limit, limsup, upper limit and outer limit.
  • DiscreteMaxLimit computes the smallest upper bound for the limit and is always defined for real-valued sequences. It is often used to give conditions of convergence and other asymptotic properties that do not rely on an actual limit to exist.
  • DiscreteMaxLimit[f,k∞] can be entered as 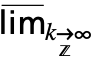f. A template 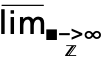can be entered as dMlim, and moves the cursor from the underscript to the body.
  • DiscreteMaxLimit[f,{k1,…,kn}{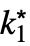,…,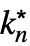}] can be entered as 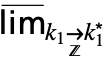…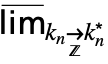f.
  • The possible limit points 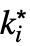are ±∞.
  • The max limit is defined as a limit of the max envelope sequence max[ω]:
  • DiscreteMaxLimit[f,k∞]DiscreteLimit[max[ω],ω∞]
    DiscreteMaxLimit[f,{k1,…,kn}{∞,…,∞}]DiscreteLimit[max[ω],ω∞]
  • DiscreteMaxLimit[f[k],k-∞] is equivalent to DiscreteMaxLimit[f[-l],l∞] etc.
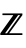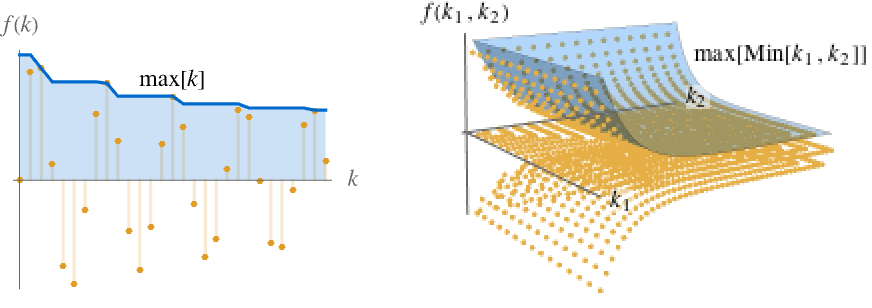
  • The definition uses the max envelope max[ω]MaxValue[{f[k],k≥ω∧k∈},k] for univariate f[k] and max[ω]MaxValue[{f[k1,…,kn],k1≥ω∧⋯∧kn≥ω∧ki∈},{k1,…,kn}] for multivariate f[k1,…,kn]. The sequence max[ω] is monotone decreasing as ω∞, so it always has a limit, which may be ±∞.
  • The illustration shows max[k] and max[Min[k1,k2]] in blue.
  • DiscreteMaxLimit returns unevaluated when the max limit cannot be found.
  • The following options can be given:
  • Assumptions $Assumptionsassumptions on parameters
    GenerateConditions Automaticwhether to generate conditions on parameters
    Method Automaticmethod to use
    PerformanceGoal "Quality"aspects of performance to optimize
  • Possible settings for GenerateConditions include:
  • Automaticnon-generic conditions only
    Trueall conditions
    Falseno conditions
    Nonereturn unevaluated if conditions are needed
  • Possible settings for PerformanceGoal include $PerformanceGoal, "Quality" and "Speed". With the "Quality" setting, DiscreteMaxLimit typically solves more problems or produces simpler results, but it potentially uses more time and memory.

Examples

open allclose all

Basic Examples  (4)Summary of the most common use cases

Max limit of a sequence:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-dab3pa
Out[1]=1

Max limit of a product:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-naxyuq
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-cz9c26
Out[2]=2

Use dMlim to enter the template and to move from the underscript to the body:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-e1mcaw
Out[1]=1

TraditionalForm typesetting:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-e82anr

Scope  (21)Survey of the scope of standard use cases

Basic Uses  (4)

Compute the max limit of a sequence when n approaches Infinity:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-hb5uiw
Out[1]=1

Compute the max limit of a sequence when n approaches -Infinity:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-et7bpy
Out[1]=1

Compute a nested max limit for a multivariate sequence:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-pukp4y
Out[1]=1

Compute the max limit of a list of sequences:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-g45pgr
Out[1]=1

Elementary Sequences  (6)

Find the max limit of a rational-exponential sequence:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-lxbke9
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-c6vm2a
Out[2]=2

Convergent geometric sequence:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-dc9wk
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-f0lb99
Out[2]=2

Oscillating geometric sequence:

In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-b9ebzb
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/01y38mtr9uq-bs2twv
Out[4]=4

Divergent oscillating geometric sequence:

In[5]:=5
✖
https://wolfram.com/xid/01y38mtr9uq-q2dwr
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/01y38mtr9uq-g2hriz
Out[6]=6

Exponential sequence:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-fxkte2
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-ek16lf
Out[2]=2

Power sequence:

In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-i5h5nm
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/01y38mtr9uq-kguw6m
Out[4]=4

Trigonometric sequences:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-e5uei
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-dm6ege
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-ml1zl
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/01y38mtr9uq-g527az
Out[4]=4

Inverse trigonometric sequence:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-lykjl
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-yzua9
Out[2]=2

Logarithmic sequence:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-8qd0z
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-i4pw3x
Out[2]=2

Periodic Sequences  (3)

Limits of periodic sequences:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-clh32t
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-ilo0ri
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-f0qvyn
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/01y38mtr9uq-egrxv
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/01y38mtr9uq-d03d2h
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/01y38mtr9uq-gnytrw
Out[6]=6

Eventually periodic sequence:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-cpqsv5
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-k12ere
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-fo2erm
Out[3]=3

Densely aperiodic sequences:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-d7z025
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-k07f3o
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-lmhs11
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/01y38mtr9uq-eagvn6
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/01y38mtr9uq-bzcdcc
Out[5]=5

Piecewise Sequences  (2)

Piecewise sequence with a finite max limit:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-vznig
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-kkguvr
Out[2]=2

Piecewise sequence with an infinite max limit:

In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-xejfm
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/01y38mtr9uq-m4nvru
Out[4]=4

Piecewise sequence with periodic conditions:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-d9ybuq
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-skkms
Out[2]=2

Special Function Sequences  (2)

Compute the limit of a sequence involving Fibonacci:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-bcqotc
Out[1]=1

Sequence involving FactorialPower:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-bof7hm
Out[1]=1

Number Theoretic Sequences  (2)

Limits involving LCM and GCD:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-b1qh0b
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-bitj2u
Out[2]=2

Sequence involving Prime:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-fsldo
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-c9987h
Out[2]=2

Multivariate Sequences  (2)

Compute a nested max limit:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-b08k82
Out[1]=1

Plot the sequence and its limit:

In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-bx7d8j
Out[2]=2

Multivariate max limits:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-yctew
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-icispr
Out[2]=2

Options  (6)Common values & functionality for each option

Assumptions  (1)

Specify assumptions on a parameter:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-e8anyf
Out[1]=1

Different assumptions can produce different results:

In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-hwqo5k
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-bwcs4h
Out[3]=3

GenerateConditions  (3)

Return a result without stating conditions:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-spbhce
Out[1]=1

This result is only valid if x>1:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-lftbu6
Out[1]=1

Return unevaluated if the results depend on the value of parameters:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-2lepxp
Out[1]=1

By default, conditions are generated that return a unique result:

In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-14nrvk
Out[2]=2

By default, conditions are not generated if only special values invalidate the result:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-uhm6gw
Out[1]=1

With GenerateConditions->True, even these non-generic conditions are reported:

In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-291b1m
Out[2]=2

Method  (1)

Compute the max limit of a periodic sequence using the default method:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-gna87y
Out[1]=1

Obtain the same answer using the method for periodic sequences:

In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-jt0cjx
Out[2]=2

The limit of the sequence is undefined, since it oscillates between 0 and 1:

In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-eqc0mj
Out[3]=3

PerformanceGoal  (1)

DiscreteMaxLimit computes limits involving sequences of arbitrarily large periods:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-i86kxj
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-i9gq
Out[2]=2

Use PerformanceGoal to avoid potentially expensive computations in such cases:

In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-byiylb
Out[3]=3

The Method option overrides PerformanceGoal:

In[4]:=4
✖
https://wolfram.com/xid/01y38mtr9uq-bh9kxc
Out[4]=4

Applications  (7)Sample problems that can be solved with this function

Basic Applications  (2)

Compute the asymptotic supremum of a sequence:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-evnfw9
Out[1]=1

Plot the sequence and the asymptotic supremum:

In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-dxedrx
Out[2]=2

Verify that the following sequence does not have a limit:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-cy4wh5
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-bibaa2
Out[2]=2

Show that DiscreteMaxLimit and DiscreteMinLimit are not equal:

In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-wrhna
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/01y38mtr9uq-d48yo1
Out[4]=4

Confirm that the limit does not exist by using DiscreteLimit:

In[5]:=5
✖
https://wolfram.com/xid/01y38mtr9uq-esjhm8
Out[5]=5

Series Convergence  (4)

Show that the infinite series whose general term is defined here is convergent, by using the ratio test:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-ev7n4k

Plot the partial sums of the series:

In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-b0n3f2
Out[2]=2

Compute the ratio of the adjacent terms using DiscreteRatio:

In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-ftt7fr
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/01y38mtr9uq-lpiz8n
Out[4]=4

The sequence of ratios does not converge:

In[5]:=5
✖
https://wolfram.com/xid/01y38mtr9uq-o22sii
Out[5]=5

However, the ratio test can still be used because the upper limit of the ratios is less than 1:

In[6]:=6
✖
https://wolfram.com/xid/01y38mtr9uq-ce96i8
Out[6]=6

Confirm that the series converges using SumConvergence:

In[7]:=7
✖
https://wolfram.com/xid/01y38mtr9uq-ij31w3
Out[7]=7

Evaluate the infinite series:

In[8]:=8
✖
https://wolfram.com/xid/01y38mtr9uq-dhyvmm
Out[8]=8
In[9]:=9
✖
https://wolfram.com/xid/01y38mtr9uq-e9vww
Out[9]=9

Show that the infinite series whose general term is defined here is convergent, by using the root test:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-j70cq

Plot the partial sums of the series:

In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-ldtgnv
Out[2]=2

Compute the n^(th) root of the general term:

In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-qo2fu
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/01y38mtr9uq-gziv33
Out[4]=4

The limit of the sequence of roots does not exist:

In[5]:=5
✖
https://wolfram.com/xid/01y38mtr9uq-vzj6wt
Out[5]=5

However, the root test still indicates convergence because the max limit is less than 1:

In[6]:=6
✖
https://wolfram.com/xid/01y38mtr9uq-hsw6yr
Out[6]=6

Confirm that the series converges using SumConvergence:

In[7]:=7
✖
https://wolfram.com/xid/01y38mtr9uq-bsw5pq
Out[7]=7

Evaluate the infinite series:

In[8]:=8
✖
https://wolfram.com/xid/01y38mtr9uq-dvuz1i
Out[8]=8

Consider the sequence :

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-kxdmo

The inverse radius of the associated power series is given by:

In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-gd1yox
Out[2]=2

This means the radius of convergence is infinite and converges for all z in TemplateBox[{}, Complexes], in particular to :

In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-qdlqle
Out[3]=3

Compute the Taylor series at zero and its radius of convergence for the following function:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-dn3iyp

The ^(th) Taylor coefficient is :

In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-zl1jxx
Out[2]=2

Formally, the Taylor series does sum to the original function:

In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-iwavm9
Out[3]=3

The radius of convergence of the Taylor series is given by:

In[4]:=4
✖
https://wolfram.com/xid/01y38mtr9uq-nd4acj
Out[4]=4

This means the Taylor series will converge for values of within of the origin. For example, at :

In[5]:=5
✖
https://wolfram.com/xid/01y38mtr9uq-0o0qzk
Out[5]=5

At values of further away, the sum will not converge; for example, at :

In[6]:=6
✖
https://wolfram.com/xid/01y38mtr9uq-ta7ac2
Out[6]=6

At the points , the terms of the Taylor series alternate between and :

In[7]:=7
✖
https://wolfram.com/xid/01y38mtr9uq-didyk7
Out[7]=7

Hence the partial sums go between and :

In[8]:=8
✖
https://wolfram.com/xid/01y38mtr9uq-kpnxvw
Out[8]=8

Visualize and the partial sums of its Taylor series on the interval ; in the interior of the interval, convergence is rapid, but the Taylor polynomials always go to either or at the endpoints:

In[9]:=9
✖
https://wolfram.com/xid/01y38mtr9uq-gylys6
Out[9]=9

Computational Complexity  (1)

An algorithm runtime function is said to be "big-o of ", written , if _(n->_(TemplateBox[{}, Integers])infty) (f(n))/(g(n))<infty:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-mlj236

Similarly, is said to be "big-theta of ", written if _(n->_(TemplateBox[{}, Integers])infty) (f(n))/(g(n))<infty and _(n->_(TemplateBox[{}, Integers])infty)(f(n))/(g(n))>0:

In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-ofku20

The statement is always true:

In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-bv5n1w
Out[3]=3

If and , then :

In[4]:=4
✖
https://wolfram.com/xid/01y38mtr9uq-n96r3n
Out[7]=7

It is possible for two functions to share neither relationship:

In[8]:=8
✖
https://wolfram.com/xid/01y38mtr9uq-dy4l4s
Out[10]=10

Hence, defines a reflexive partial order on the space of algorithm runtimes similar to :

In[11]:=11
✖
https://wolfram.com/xid/01y38mtr9uq-r95me4
In[12]:=12
✖
https://wolfram.com/xid/01y38mtr9uq-sh3ntl
Out[12]=12

If and , then , which implies that is an equivalence relation:

In[13]:=13
✖
https://wolfram.com/xid/01y38mtr9uq-dezmtj
Out[15]=15

Properties & Relations  (11)Properties of the function, and connections to other functions

A real-valued sequence always has a (possibly infinite) max limit:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-dqn5f4
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-ejovu
Out[2]=2

The corresponding limit may not exist:

In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-9h2du
Out[3]=3

If and have finite max limits, then TemplateBox[{{(, {f, +, g}, )}, x, a}, DiscreteMaxLimit]<=TemplateBox[{f, x, a}, DiscreteMaxLimit]+TemplateBox[{g, x, a}, DiscreteMaxLimit]:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-hapf7s
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-ki9asl
In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-hoyphw
Out[3]=3

In this case, there is strict inequality:

In[4]:=4
✖
https://wolfram.com/xid/01y38mtr9uq-4wm4fg
Out[4]=4

Positive multiplicative constants can be moved outside a limit:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-bytgex
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-fv4gx
In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-crrr33
Out[3]=3

For a real-valued sequence, if DiscreteLimit exists, DiscreteMaxLimit has the same value:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-djj1nf
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-tlom4
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-bb2v
Out[3]=3

If has a finite limit, then TemplateBox[{{(, {f, +, g}, )}, x, a}, DiscreteMaxLimit]=TemplateBox[{f, x, a}, DiscreteMaxLimit]+TemplateBox[{g, x, a}, DiscreteMaxLimit]:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-hfqnkd
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-jeu5t4
In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-5nd1ru
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/01y38mtr9uq-hi3dhc
Out[4]=4

DiscreteMaxLimit is always greater than or equal to DiscreteMinLimit:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-othtxe
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-0p8t57
Out[2]=2

If DiscreteMaxLimit equals DiscreteMinLimit, the limit exists and equals their common value:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-f6hztd
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-bvlaz9
Out[2]=2

If the max limit is , then the min limit and thus the limit are also :

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-tw9zq1
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-1z7ub5
Out[2]=2

DiscreteMaxLimit can be computed as -DiscreteMinLimit[-f,…]:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-5oz4gv
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-mse78t
Out[2]=2

If , then TemplateBox[{{g, (, n, )}, x, a}, MaxLimit2Arg]<=TemplateBox[{{f, (, n, )}, x, a}, MinLimit2Arg]<=TemplateBox[{{f, , {(, n, )}}, x, a}, MaxLimit2Arg]:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-zwywc
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-g2avgr
In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-wbzb2v
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/01y38mtr9uq-k7j3pk
Out[4]=4

If the two max limits are equal—as in this example—then has a limit:

In[5]:=5
✖
https://wolfram.com/xid/01y38mtr9uq-vnttqn
Out[5]=5

This is a generalization of the "squeezing" or "sandwich" theorem:

In[6]:=6
✖
https://wolfram.com/xid/01y38mtr9uq-b1meus
Out[6]=6

MaxLimit is always greater than or equal to DiscreteMaxLimit:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-58ji5s
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-34gpyb
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-qtl6qs
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/01y38mtr9uq-uu7jv3
Out[4]=4

Possible Issues  (1)Common pitfalls and unexpected behavior

DiscreteMaxLimit is only defined for real-valued sequences:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-kyusc
Out[1]=1

Neat Examples  (1)Surprising or curious use cases

Visualize a set of sequence max limits:

In[1]:=1
✖
https://wolfram.com/xid/01y38mtr9uq-cd80wk
In[2]:=2
✖
https://wolfram.com/xid/01y38mtr9uq-hq7d3z
In[3]:=3
✖
https://wolfram.com/xid/01y38mtr9uq-xvse5
Out[3]=3
Wolfram Research (2017), DiscreteMaxLimit, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html.
✖
Wolfram Research (2017), DiscreteMaxLimit, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html.

Text

Wolfram Research (2017), DiscreteMaxLimit, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html.

✖
Wolfram Research (2017), DiscreteMaxLimit, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html.

CMS

Wolfram Language. 2017. "DiscreteMaxLimit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html.

✖
Wolfram Language. 2017. "DiscreteMaxLimit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html.

APA

Wolfram Language. (2017). DiscreteMaxLimit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html

✖
Wolfram Language. (2017). DiscreteMaxLimit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html

BibTeX

@misc{reference.wolfram_2025_discretemaxlimit, author="Wolfram Research", title="{DiscreteMaxLimit}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html}", note=[Accessed: 01-April-2025 ]}

✖
@misc{reference.wolfram_2025_discretemaxlimit, author="Wolfram Research", title="{DiscreteMaxLimit}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html}", note=[Accessed: 01-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_discretemaxlimit, organization={Wolfram Research}, title={DiscreteMaxLimit}, year={2017}, url={https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html}, note=[Accessed: 01-April-2025 ]}

✖
@online{reference.wolfram_2025_discretemaxlimit, organization={Wolfram Research}, title={DiscreteMaxLimit}, year={2017}, url={https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html}, note=[Accessed: 01-April-2025 ]}