DiscreteLimit

DiscreteLimit[f,k∞]

gives the limit k∞f(k) for the sequence f as k tends to infinity over the integers.

DiscreteLimit[f,{k1,…,kn}]

gives the nested limit ⋯ f(k1,…,kn) over the integers.

DiscreteLimit[f,{k1,…,kn}{,…,}]

gives the multivariate limit f(k1,…,kn) over the integers.

Details and Options

  • DiscreteLimit is also known as discrete limit or limit over the integers.
  • DiscreteLimit computes the limiting value of a sequence f as its variables k or ki get arbitrarily large.
  • DiscreteLimit[f,k∞] can be entered as 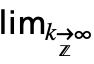f. A template 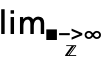can be entered as dlim, and moves the cursor from the underscript to the body.
  • DiscreteLimit[f,{k1,…,kn}{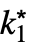,…,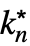}] can be entered as 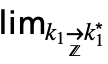…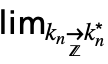f.
  • The possible limit points 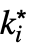are ±∞.
  • For a finite limit value f*:
  • DiscreteLimit[f,k∞]f*for every 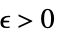there is a 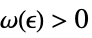such that 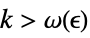implies TemplateBox[{{{f, (, k, )}, -, {f, ^, *}}}, Abs]<epsilon
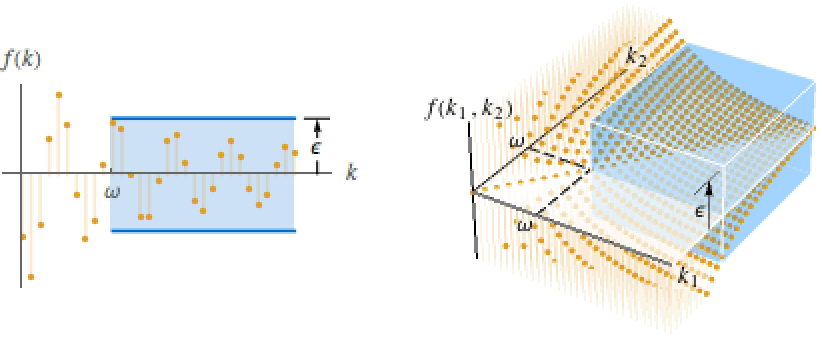
    DiscreteLimit[f,{k1,…,kn}{∞,…,∞}]f*for every 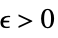there is a 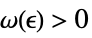such that 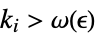implies TemplateBox[{{{f, (, {{k, _, 1}, ,, ..., ,, {k, _, n}}, )}, -, {f, ^, *}}}, Abs]<epsilon
  • DiscreteLimit[f[k],k-∞] is equivalent to DiscreteLimit[f[-l],l∞] etc.
  • DiscreteLimit returns Indeterminate when it can prove that the limit does not exist, and returns unevaluated when no limit can be found.
  • The following options can be given:
  • Assumptions $Assumptionsassumptions on parameters
    GenerateConditions Automaticwhether to generate conditions on parameters
    Method Automaticmethod to use
    PerformanceGoal "Quality"aspects of performance to optimize
  • Possible settings for GenerateConditions include:
  • Automaticnon-generic conditions only
    Trueall conditions
    Falseno conditions
    Nonereturn unevaluated if conditions are needed
  • Possible settings for PerformanceGoal include $PerformanceGoal, "Quality" and "Speed". With the "Quality" setting, DiscreteLimit typically solves more problems or produces simpler results, but it potentially uses more time and memory.

Examples

open allclose all

Basic Examples  (4)

Limit of a sequence:

Plot the sequence and its limit:

Limit of a multivariate sequence:

Plot the sequence and its limit:

Use dlim to enter the template and to move from the underscript to the body:

TraditionalForm typesetting:

Scope  (37)

Basic Uses  (4)

Compute the limit of a sequence when n approaches Infinity:

Compute the limit of a sequence when n approaches -Infinity:

Compute a nested limit for a multivariate sequence:

Compute the limit of a list of sequences:

Elementary Function Sequences  (7)

Find the limit of a rational sequence:

Geometric sequence:

Exponential sequences:

Trigonometric sequence:

Inverse trigonometric sequence:

Logarithmic sequence:

Find the limit of ArcTan[Log[n]]:

Integer Function Sequences  (5)

Compute the limit of a binomial sequence:

Limits of sequences involving FactorialPower:

Limits of sequences involving Factorial:

Compute limits involving Fibonacci and LucasL:

Limit involving Pochhammer:

Alternating Sequences  (3)

Convergent alternating sequence:

Divergent alternating sequence:

Oscillatory alternating sequence:

Periodic Sequences  (3)

Limits involving periodic sequences:

Eventually periodic sequence:

Densely aperiodic sequences:

Piecewise Function Sequences  (3)

A convergent piecewise sequence:

A divergent piecewise sequence:

Piecewise sequence with periodic conditions:

Limit involving Floor:

Number Theoretic Function Sequences  (4)

Compute limits involving Prime:

Prime is of order :

Limits involving PrimePi:

PrimePi is of order :

Limits involving PartitionsP and PartitionsQ:

Limits involving other number theoretic sequences:

Nested and Multivariate Sequences  (2)

Compute a nested sequence limit:

Plot the sequence and its limit:

Multivariate sequence limits:

Formal Sequences  (6)

Compute limits of sequences involving Inactive sums:

Nested limit of an Inactive sum:

Obtain the same result in two steps using an interchange of DiscreteLimit and Sum:

Limits of sequences involving Inactive products:

Nested limit of an Inactive product:

Obtain the same result in two steps using an interchange of DiscreteLimit and Product:

Limits of sequences involving Inactive continued fractions:

Nested limit of an Inactive continued fraction:

Obtain the same result in two steps using DiscreteLimit and ContinuedFractionK:

Options  (6)

Assumptions  (1)

Specify assumptions on a parameter:

Different assumptions can produce different results:

GenerateConditions  (3)

Return a result without stating conditions:

This result is only valid if y>1:

Return unevaluated if the results depend on the value of parameters:

By default, conditions are generated that return a unique result:

By default, conditions are not generated if only special values invalidate the result:

With GenerateConditions->True, even these non-generic conditions are reported:

Method  (1)

Compute the limit of a sequence using the default method:

Obtain the same answer using a call to Limit:

The given sequence is not periodic, hence the method for periodic sequences fails:

PerformanceGoal  (1)

DiscreteLimit computes limits involving sequences of arbitrarily large periods:

Use PerformanceGoal to avoid potentially expensive computations in such cases:

The Method option overrides PerformanceGoal:

Applications  (35)

Geometric Limits  (3)

The perimeter of a regular polygon of radius r and n sides:

In the limit n->∞, the perimeter approaches the circumference of a circle of radius r:

The area of a regular polygon of radius r and n sides:

In the limit n->∞, this approaches the area of a circle of radius r:

Visualize the inscribed polygon and the approximate perimeter and area as n increases:

Consider covering a ball of radius r by 2n cylinders as shown in the figure:

The volume of the cylinders is:

Taking the DiscreteLimit as n->Infinity gives the volume of the ball:

Compare with a direct computation:

Consider the following function and a set of rectangles defined by its plot:

For n5 on the interval [0,2], the rectangles are the following:

The area of these rectangles defines a Riemann sum that approximates the area under the curve:

Use DiscreteLimit to obtain the exact answer:

Obtain the same area directly using Integrate:

Visualize the process for this function as well as three others:

Sums and Products  (6)

Compute an infinite sum as the limit of a finite sum:

Obtain the same answer using Sum:

The following sequence defines a convergent series:

Find the value of the series:

Compute the result directly using Sum:

Prove that an infinite series is divergent, starting with the sum of a finite number of terms:

The series diverges, since the limit of the finite sums does not exist:

Confirm the divergence using SumConvergence and Sum:

Obtain the Abel sum of the series using Regularization:

Compute a doubly infinite sum as a nested limit of a finite sum:

Obtain the same answer directly using Sum:

Compute an infinite product as a limit of a finite product:

Obtain the same answer using Product:

Construct a rotation matrix as a limit of repeated infinitesimal transformations:

Compare with a direction construction:

Series Convergence  (4)

Use the ratio test to verify convergence of a series whose general term is given by:

Compute the DiscreteRatio for this series:

The series converges, since the limit of the ratio is less than 1:

Verify the result using SumConvergence:

Use the root test to verify convergence of a series whose general term is given by:

The series converges, since the limit of the n^(th) root is less than 1:

Verify the result using SumConvergence:

Use the Raabe test to verify convergence of a series whose general term is given by:

Raabe's test applies because the ratio test is inconclusive:

The series converges, since the following limit is greater than 1:

Verify the result using SumConvergence:

Use the divergence test to verify divergence of a series whose general term is given by:

The series diverges, since the limit of the general term is not 0:

Verify the result using SumConvergence:

Classical Definition  (3)

Show that the following sequence converges to 0, and verify the classical definition with ϵ=1/7:

Compute the limit:

Set the value of :

Use Reduce to show that the definition is satisfied for all n>=12:

Verify the result using DiscretePlot:

Show that the following sequence diverges to Infinity, and verify the classical definition with M=35:

Compute the limit:

Set the value of M:

Use Reduce to show that the definition is satisfied for all n >= 10:

Verify the result using DiscretePlot:

Determine the convergence of the harmonic series , whose terms are given by:

Standard tests such as the ratio test are inconclusive:

Define an auxiliary series as follows:

The terms of consist of runs of length of :

Notice that :

Also, the sum of each run is , so the sum of the first terms is :

The partial sums of are called the harmonic numbers TemplateBox[{n}, HarmonicNumber]:

For any positive integer , TemplateBox[{{2, ^, {(, {{2, , M}, -, 2}, )}}}, HarmonicNumber]>=sum_(n=1)^(2^(2 M-2))a(n)=M, so TemplateBox[{n}, HarmonicNumber] eventually exceeds and diverges to :

This means the sum of does not converge:

The divergence is slow, however, requiring more than terms just to get over :

Recursive Sequences  (3)

Compute the limit of a nonlinear recursive sequence that is specified using RSolveValue:

Compute the limit of a trigonometric recursive sequence that is specified using RSolveValue:

Compute the value of :

Mathematical Constants  (5)

Compute as the limit of a sequence:

Compute as the limit of a Sum:

Compute as the limit of a sequence:

Compute EulerGamma using the limit of a sequence:

Compute the golden ratio using a sequence involving Fibonacci:

Mathematical Functions  (2)

Represent as the limit of a sequence with symbolic entries:

Represent Log[x] as the limit of a sequence:

Stolz–Cesàro Theorem  (2)

The Stolz–Cesàro theorem is a discrete version of L'Hôpital's rule, and can be used to compute the limits for ratios of sequences, under suitable conditions. The theorem states that:

Verify the Stolz–Cesàro theorem for the sequences defined by:

Compute the limit for the ratio of differences:

Obtain the same result directly using DiscreteLimit:

Plot the sequence and the limit:

Verify the Stolz–Cesàro theorem for the sequences defined by:

Compute the limit for the ratio of differences:

Obtain the same result directly using DiscreteLimit:

Plot the sequence and the limit:

Computational Complexity  (3)

An algorithm runtime function is said to be "little-o of ", written , if :

Similarly, is said to be "little-omega of ", written , if :

If , then :

It is possible for two functions to share neither relationship:

Moreover, neither relationship even holds between a function and itself:

Hence, and define partial orders on the space of algorithm runtimes:

if the algorithm associated to is much faster than the one associated to for large inputs:

denotes the opposite relationship:

Note that the two lists are not exactly reversed, because and are incomparable:

An algorithm runtime function is said to be "big-theta of ", written , if the following holds:

Consider an algorithm that takes time —a polynomial of degree —to run:

The ratio of this function to the monomial goes to the leading coefficient at infinity:

Since the limit of the sequence exists, its max and min limits must both equal this value:

For an algorithmic runtime, must be a positive finite number, so every polynomial algorithm is :

Hence, only the leading term in the polynomial is important in determining the runtime for large inputs:

Check the asymptotic complexity of the fast Fourier transform:

Compute the asymptotic complexity:

Uniform Convergence  (2)

At every point , the following sequence of functions converges to zero:

The greatest magnitude of each is achieved at :

Thus, for any , implies that TemplateBox[{{{f, _, n}, (, x, )}}, RealAbs]<epsilon for all and the convergence is uniform:

As a consequence, the limit of the integrals equals the integral of the limit:

At every point , the following sequence of functions converges to zero:

However, the maximum value of , at the point , diverges as :

This shows that the convergence of the sequence of functions is not uniform:

As a consequence, the limit of the integrals does not equal the integral of the limit:

Miscellaneous Applications  (2)

Compute the inverse Laplace transform of using Post's inversion formula:

The inverse Laplace transform of this function is 1:

Obtain the same result using InverseLaplaceTransform:

Create a table of basic inverse Laplace transforms using Post's inversion formula:

The limit of the probability distribution for a sequence of random variables, if it exists, is called an asymptotic distribution. Obtain the Poisson distribution as an asymptotic distribution for a sequence of binomial distributions in which the mean value λ, the product of the probability and number of trials, is held constant:

Compute the limit of this sequence as the number of trials n->∞:

Verify that this is the PDF for PoissonDistribution:

Plot the distributions for λ=8 and various values of n. Notice that the PDF is zero for all k>n:

Properties & Relations  (15)

Multiplicative constants can be moved outside a limit:

If f and g have finite limits, DiscreteLimit is distributive over a sum:

If f and g have finite limits, DiscreteLimit is distributive over a product:

Powers can be moved outside a limit:

Function composition and sequence limit operations can be interchanged for continuous functions:

This need not hold for discontinuous functions:

The "squeezing" or "sandwich" theorem:

This function is bounded by on the positive integers:

The limit of the bounding functions is zero, which proves the original limit was zero:

The Stolz–Cesàro rule can be used to find the limit of the ratio of two sequences:

Directly solving the limit leads to an indeterminate form of type :

The Stolz–Cesàro rule is applied to correctly compute the limit:

If Limit exists, then so does DiscreteLimit, and they have the same value:

The converse need not hold:

If DiscreteLimit exists, then so does DiscreteMaxLimit, and they have the same value:

If DiscreteLimit exists, then so does DiscreteMinLimit, and they have the same value:

The limit of a difference satisfies TemplateBox[{{{f, (, {n, +, 1}, )}, -, {f, (, n, )}}, n, infty}, DiscreteLimit]=TemplateBox[{{{(, {f, (, n, )}, )}, /, n}, n, infty}, DiscreteLimit]:

The limit of a ratio satisfies TemplateBox[{{{(, {f, (, {n, +, 1}, )}, )}, /, {(, {f, (, n, )}, )}}, n, infty}, DiscreteLimit]=TemplateBox[{{{f, (, n, )}, ^, {(, {1, /, n}, )}}, n, infty}, DiscreteLimit]:

Compute the limit of a sequence using a finite sum:

Compute the limit of a sequence using a finite product:

The limit of a sequence is related to its ZTransform via the final value theorem:

Verify the final value theorem:

Neat Examples  (1)

Visualize a set of sequence limits:

Wolfram Research (2017), DiscreteLimit, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteLimit.html.

Text

Wolfram Research (2017), DiscreteLimit, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteLimit.html.

CMS

Wolfram Language. 2017. "DiscreteLimit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteLimit.html.

APA

Wolfram Language. (2017). DiscreteLimit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteLimit.html

BibTeX

@misc{reference.wolfram_2025_discretelimit, author="Wolfram Research", title="{DiscreteLimit}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteLimit.html}", note=[Accessed: 18-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_discretelimit, organization={Wolfram Research}, title={DiscreteLimit}, year={2017}, url={https://reference.wolfram.com/language/ref/DiscreteLimit.html}, note=[Accessed: 18-April-2025 ]}