DiscreteUniformDistribution[{imin,imax}]
represents a discrete uniform distribution over the integers from imin to imax.
DiscreteUniformDistribution[{{imin,imax},{jmin,jmax},…}]
represents a multivariate discrete uniform distribution over integers within the box {{imin,imax},{jmin,jmax},…}.


DiscreteUniformDistribution
DiscreteUniformDistribution[{imin,imax}]
represents a discrete uniform distribution over the integers from imin to imax.
DiscreteUniformDistribution[{{imin,imax},{jmin,jmax},…}]
represents a multivariate discrete uniform distribution over integers within the box {{imin,imax},{jmin,jmax},…}.
Details
- DiscreteUniformDistribution is also known as discrete rectangular distribution.
- The probability for value
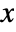 in a discrete uniform distribution is constant for integers
in a discrete uniform distribution is constant for integers 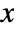 such that
such that 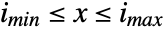 , and is zero otherwise. »
, and is zero otherwise. » - DiscreteUniformDistribution allows imin and imax to be any integers such that imin<imax.
- DiscreteUniformDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- DiscreteUniformDistribution[{imin,imax}] represents a discrete statistical distribution (sometimes also known as the discrete rectangular distribution) in which a random variate is equally likely to take any of the integer values
 . Consequently, the uniform distribution is parametrized entirely by the endpoints imin and imax of its domain, and its probability density function is constant on the integers within the interval
. Consequently, the uniform distribution is parametrized entirely by the endpoints imin and imax of its domain, and its probability density function is constant on the integers within the interval 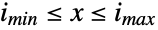 . The discrete uniform distribution is the discretized version of UniformDistribution, and like the latter, the discrete uniform distribution also generalizes to multiple variates, each of which is equally likely on some domain.
. The discrete uniform distribution is the discretized version of UniformDistribution, and like the latter, the discrete uniform distribution also generalizes to multiple variates, each of which is equally likely on some domain. - The likelihood of rolling any single value k from a fair die is precisely modeled by PDF[DiscreteUniformDistribution[{1,6}],k]. Given a key ring containing a unique correct key together with n incorrect ones, a modification of the inverse transform method using a discrete random variable on values 1,…,n can be used to model the number of incorrect distinct selections expected before finding the correct key. This problem is related to the so-called estimation of maximum problem. An example of this known as the German tank problem was important in World War II and involved estimating the maximum
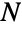 needed in order for DiscreteUniformDistribution[{1,N}] to yield k observations for some integer k,
needed in order for DiscreteUniformDistribution[{1,N}] to yield k observations for some integer k, 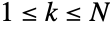 .
. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a discrete uniform distribution. Distributed[x,DiscreteUniformDistribution[{imin,imax}]], written more concisely as xDiscreteUniformDistribution[{imin,imax}], can be used to assert that a random variable x is distributed according to a discrete uniform distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[DiscreteUniformDistribution[{imin,imax}],x] and CDF[DiscreteUniformDistribution[{imin,imax}],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. These quantities can be visualized using DiscretePlot.
- DistributionFitTest can be used to test if a given dataset is consistent with a discrete uniform distribution, EstimatedDistribution to estimate a discrete uniform parametric distribution from given data, and FindDistributionParameters to fit data to a discrete uniform distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic discrete uniform distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic discrete uniform distribution.
- TransformedDistribution can be used to represent a transformed discrete uniform distribution. Additionally, CopulaDistribution can be used to build higher-dimensional distributions that contain a discrete uniform distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving discrete uniform distributions.
- The discrete uniform distribution is related to a number of other distributions. For example, DiscreteUniformDistribution[{a,b}] is the discretized version of UniformDistribution[{a,b}] under the assumption that both a and b are integers. DiscreteUniformDistribution is also related to PoissonDistribution in the sense that the sum
 of n independent discrete uniformly distributed random variables
of n independent discrete uniformly distributed random variables  where nPoissonDistribution is itself a transformed Poisson distribution. The discrete uniform distribution is related to GeometricDistribution, due to the fact that if (x1x1+x2)DiscreteUniformDistribution, then xiGeometricDistribution for
where nPoissonDistribution is itself a transformed Poisson distribution. The discrete uniform distribution is related to GeometricDistribution, due to the fact that if (x1x1+x2)DiscreteUniformDistribution, then xiGeometricDistribution for 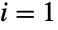 and 2. DiscreteUniformDistribution is also related to BetaBinomialDistribution and tangentially to distributions such as CompoundPoissonDistribution.
and 2. DiscreteUniformDistribution is also related to BetaBinomialDistribution and tangentially to distributions such as CompoundPoissonDistribution.
Examples
open all close allBasic Examples (3)
Scope (14)
Probability density function of a bivariate discrete uniform distribution:
Cumulative distribution function of a bivariate discrete uniform distribution:
Generate a sample of pseudorandom numbers from a discrete uniform distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Distribution parameters estimation for a multivariate discrete uniform distribution:
Estimate the distribution parameters from sample data:
With an infinitely large interval, the kurtosis equals the kurtosis of UniformDistribution:
Multivariate discrete uniform distribution:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Closed form for symbolic order:
Closed form for symbolic order:
Different mixed moments for a multivariate discrete uniform distribution:
Closed form for symbolic order:
Closed form for symbolic order:
Closed form for symbolic order:
Closed form for symbolic order:
Hazard function of univariate discrete uniform distribution:
Median of a univariate discrete uniform distribution:
The marginals of a multivariate discrete uniform distribution are discrete uniform distributions:
Applications (7)
The CDF of DiscreteUniformDistribution is an example of a right-continuous function:
A computer has four disks, numbered 0, 1, 2, 3, one of which is chosen at random on boot to store temporary files. Find the distribution of the chosen disk:
Find the probability that disk 1 is chosen:
Find the probability that an odd-numbered disk is chosen:
Simulate which disk is chosen on the next 30 boots:
A fair six-sided die can be modeled using a DiscreteUniformDistribution:
Generate 10 throws of the die:
Compute the probability that the sum of three dice values is less than 6:
Verify by generating random dice throws, in this case ![]() times three dice throws:
times three dice throws:
Verify by explicitly enumerating all possible dice outcomes:
Two fair dice are tossed. Find the distribution of the difference of the dice values:
Find the probability that the difference is at most 3:
Simulate differences for the 30 tosses:
In the game of craps [MathWorld], two dice are thrown:
The resulting PDF can be tabulated as:
Find the probability of getting "snake eyes" [MathWorld]:
Or "boxcars" [MathWorld]:
Or "eighter from Decatur" [MathWorld]:
Or "little Joe" [MathWorld]:
The full list of probabilities:
Find the probability of losing in one throw or getting craps, i.e. any of the sums 2, 3, or 12:
Find the probability of winning in one throw, i.e. getting the sums 7 or 11:
A hypothetical R&D company has a holiday whenever at least one employee has a birthday. Find the number of employees that maximizes the days worked, assuming independent distributions of birthdays:
Find the optimal number of employees:
Solve Galileo's problem to determine the odds of getting 9 points versus 10 points obtained in throws of three dice:
Although the number of integer partitions of 10 and 9 into a sum of three numbers 1–6 are the same:
Properties & Relations (4)
The probability of getting any real number except an integer between min and max is zero:
The components of multivariate discrete uniform distribution are uncorrelated:
DiscreteUniformDistribution is the discrete analog of UniformDistribution:
Possible Issues (2)
DiscreteUniformDistribution is not defined when min or max is not an integer:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
See Also
Tech Notes
Text
Wolfram Research (2007), DiscreteUniformDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteUniformDistribution.html (updated 2010).
CMS
Wolfram Language. 2007. "DiscreteUniformDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2010. https://reference.wolfram.com/language/ref/DiscreteUniformDistribution.html.
APA
Wolfram Language. (2007). DiscreteUniformDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteUniformDistribution.html
BibTeX
@misc{reference.wolfram_2025_discreteuniformdistribution, author="Wolfram Research", title="{DiscreteUniformDistribution}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteUniformDistribution.html}", note=[Accessed: 02-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_discreteuniformdistribution, organization={Wolfram Research}, title={DiscreteUniformDistribution}, year={2010}, url={https://reference.wolfram.com/language/ref/DiscreteUniformDistribution.html}, note=[Accessed: 02-March-2026]}