WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

ExpIntegralE

ExpIntegralE[n,z]

指数積分関数を与える．

詳細

記号操作・数値操作の両方に適した数学関数である．
積分が収束するところで $TemplateBox[{n, z}, ExpIntegralE]=int_1^inftye^(-z t)/t^ndt$ ．
ExpIntegralE[n,z]は，複素 z 平面上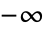，〜0の範囲で不連続な分枝切断線を持つ．
特別な引数の場合，ExpIntegralEは，自動的に厳密値を計算する．
ExpIntegralE は任意の数値精度で評価できる．
ExpIntegralE は，自動的にリストに縫い込まれる．
ExpIntegralEはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる． »

例題

すべて開くすべて閉じる

例 (5)

数値的に評価する：

実数の部分集合上でパラメータの整数値についてプロットする：

複素数の部分集合上でプロットする：

原点における一般的および対数的な場合の級数：

Infinityにおける級数展開：

スコープ (42)

数値評価 (5)

高精度で数値的に評価する：

出力の精度は入力の精度に従う：

複素引数：

ExpIntegralEを高精度で効率よく評価する：

IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する：

Aroundを使って平均的な場合の統計区間を計算することもできる：

配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のExpIntegralE関数を計算することもできる：

特定の値 (3)

固定点における値：

無限大における極限値：

方程式の実根を求める：

可視化 (3)

ExpIntegralE関数をプロットする：

の実部をプロットする：

の虚部をプロットする：

の実部をプロットする：

の虚部をプロットする：

関数の特性 (9)

ExpIntegralEの実領域：

ExpIntegralEの複素領域：

はのときすべての実数値に達する：

の小さい値についてのExpIntegralEの値域は，より制限されていることもいないこともある：

ExpIntegralEは鏡特性を持つ：

ExpIntegralEは解析関数ではない：

有理型でもない：

はのときは常に非増加である：

のときは単射である：

のより小さい値については，単射であることもそうではないこともある：

3つの例を可視化する：

のときは正である：

ExpIntegralEは x≤0のとき特異点と不連続点の両方を持つ：

はのとき凸である：

微分 (3)

一次導関数：

高次導関数：

について高次導関数をプロットする：

について高次導関数をプロットする：

次導関数の式：

積分 (3)

ExpIntegralEの不定積分：

ExpIntegralEの定積分：

その他の積分例：

級数展開： (4)

ExpIntegralEの級数展開：

周りのの最初の3つの近似をプロットする：

の級数展開における一般項：

無限大における級数展開：

任意の記号方向についての結果を与える：

ExpIntegralEはベキ級数に適用できる：

積分変換 (3)

FourierSinTransformを使ってについてのフーリエ(Fourier)正弦変換を計算する：

についてのLaplaceTransform：

MellinTransform：

関数の恒等式と簡約 (4)

FullSimplifyを使って指数積分を簡約する：

FunctionExpandを使って特殊ケースをより簡単な関数で表す：

再帰関係：

のとき：

関数表現 (5)

指数積分関数の主定義：

不完全ガンマ関数Gammaとの関係：

ExpIntegralEはMeijerGによって表すことができる：

ExpIntegralEはDifferentialRootとして表すことができる：

TraditionalFormによる表示：

一般化と拡張 (2)

無限引数は厳密な結果を与える：

ExpIntegralEは要素単位でリストや配列に縫い込まれる：

アプリケーション (5)

複素平面上でプロットする：

区分定数の初期条件での熱伝導方程式の解：

解が熱伝導方程式を満足するかどうか確かめる：

異なる時間で解をプロットする：

階乗係数を持つ古典的な漸近級数を計算する：

打ち切られた級数と指数積分和の差分をプロットする：

水文学および電子構造計算で生じる「漏出滞水層」関数（Hantush–Jacob関数または不完全ベッセル(Bessel)関数としても知られている）をExpIntegralEで級数展開を使って近似する：

定義積分の求積法と比較する：

時間に支払われる1ドルの死亡保険金の期待時間価値を計算する．ここで，はGompertz–Makeham分布から取られる：

通常は保険年度の初めに支払われる年間保険料を求めるが，これは期間 ( はGompertz–Makeham分布から取られる) の支払ストリームの期待時間価値を正味単一保険料と等しくするために必要である：

結果の正味変換保険料：

特性と関係 (8)

FullSimplifyを使って指数積分を簡約する：

FunctionExpandを使って，より簡単な関数の特殊形を表す：

超越方程式の根を数値的に求める：

積分，和，微分方程式から生成する：

ExpIntegralEは，超幾何関数およびマイヤー(Meijer)のG関数の特殊形の様に見える：

積分：

ExpIntegralEは数値関数である：

ExpIntegralEはDifferenceRootとして表すことができる：

考えられる問題 (3)

引数が大きいと，解が大きすぎて明示的に計算できないことがある：

機械数による入力だと，高精度の結果が得られることがある：

TraditionalFormでは，は，自動的には指数積分だとは解釈されない：

おもしろい例題 (1)

のリーマン(Riemann)面をプロットする：

トップへ