Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

ExpIntegralE

ExpIntegralE[n,z]

给出指数积分函数 .

更多信息

数学函数，适宜于符号和数值运算.
$TemplateBox[{n, z}, ExpIntegralE]=int_1^inftye^(-z t)/t^ndt$ ，其中的积分收敛.
ExpIntegralE[n,z] 在复平面 z 上有从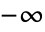到 0 的分支切割.
对于某些特殊自变量，ExpIntegralE 自动计算出精确值.
ExpIntegralE 可求任意数值精度的值.
ExpIntegralE 自动逐项作用于列表的各个元素.
ExpIntegralE 可与 Interval 和 CenteredInterval 对象一起使用. »

范例

打开所有单元关闭所有单元

基本范例 (5)

数值计算：

在实数子集绘制参数为整数的函数：

在复数的子集上绘图：

一般情形和对数情况下在原点处的级数：

在 Infinity 的级数展开：

范围 (42)

数值计算 (5)

高精度数值计算：

输出精度与输入精度相一致：

计算复数参数：

在高精度条件下高效计算 ExpIntegralE：

用 Interval 和 CenteredInterval 对象计算最坏情况下的区间：

或用 Around 计算一般情况下的统计区间：

计算数组中每个元素的值：

或用 MatrixFunction 计算矩阵形式的 ExpIntegralE 函数：

特殊值 (3)

固定点上的值：

无穷处的极限：

求方程的实根：

可视化 (3)

绘制 ExpIntegralE 函数：

绘制的实部：

绘制的虚部：

绘制的实部：

绘制的虚部：

函数属性 (9)

ExpIntegralE 的实定义域：

ExpIntegralE 的复定义域：

时，的值域是所有实数：

取较小值时，ExpIntegralE 的值域可能会也可能不会更有限：

ExpIntegralE 具有镜像属性：

ExpIntegralE 不是解析函数：

也不是亚纯函数：

时，总是非递增：

时，是单射函数：

取较小值时，可能是也可能不是单射函数：

可视化三个例子：

时，为正：

x≤0 时，ExpIntegralE 有奇点和断点：

时，是凸函数：

微分 (3)

一阶导数：

高阶导数：

绘制时的高阶导数：

绘制时的高阶导数：

阶导数的公式：

积分 (3)

ExpIntegralE 的不定积分：

ExpIntegralE 的定积分：

更多积分：

级数展开式 (4)

ExpIntegralE 的级数展开式：

绘制在处的前三个近似式：

级数展开式的通项:

在无穷处的级数展开式：

给出在任意符号方向上的结果：

ExpIntegralE 可用于幂级数：

积分变换 (3)

用 FourierSinTransform 计算的傅立叶正弦变换：

的LaplaceTransform：

MellinTransform：

函数恒等式和化简 (4)

用 FullSimplify 化简指数积分：

通过 FunctionExpand 用更简单的函数来表示特例：

递归关系式：

时，：

函数表示 (5)

指数积分函数的主定义：

与不完全伽玛函数 Gamma 的关系：

ExpIntegralE 可以被表示为 MeijerG 的形式：

ExpIntegralE 可以被表示为 DifferentialRoot：

TraditionalForm 格式：

推广和延伸 (2)

无穷参数给出精确的结果：

ExpIntegralE 按元素线性作用于列表和数组：

应用 (5)

在复平面上绘制图形：

求解分段初始条件的热方程：

检查结果是否满足热方程：

绘制不同时刻的解：

计算带有阶乘系数的经典渐近级数：

绘制被截断的级数与指数积分和的差异：

利用 ExpIntegralE 的级数展开，求水文学和电子结构计算中出现的“渗漏含水层”函数的近似（也称为 Hantush–Jacob 函数或不完全贝塞尔函数）：

与定义积分的求积比较：

计算在时间支付 1 美元的死亡保险金的预期时间值，其中从姜氏-梅约翰分布中提取：

求通常在保单年度开始时支付的年保险费，该保险费使得支付现金流在共期期间的预期时间值（其中来自姜氏-梅约翰分布）等于净单次保险费：

由此产生的年净保费：

属性和关系 (8)

用 FullSimplify 来化简指数积分：

用 FunctionExpand 来表示简单函数中的特殊条件：

求超越方程的数值根：

从积分、求和和微分方程中产生：

ExpIntegralE 显示为超几何和 Meijer G 函数的一个特例：

积分：

ExpIntegralE 是一个数值函数：

ExpIntegralE 可以被表示为 DifferenceRoot：

可能存在的问题 (3)

过大参数给出的结果太大以致无法直接计算：

机器数输入可以给出高精度结果：

在 TraditionalForm 中，不能自动解释为指数积分：

巧妙范例 (1)

绘制的黎曼面：

顶部