ExpectedValue

As of Version 8.0, ExpectedValue has been superseded by Expectation and NExpectation.

ExpectedValue[f,list]

gives the expected value of the pure function f with respect to the values in list.

ExpectedValue[f,list,x]

gives the expected value of the function f of x with respect to the values of list.

ExpectedValue[f,dist]

gives the expected value of the pure function f with respect to the symbolic distribution dist.

ExpectedValue[f,dist,x]

gives the expected value of the function f of x with respect to the symbolic distribution dist.

Details and Options

  • For the list 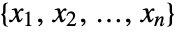, the expected value of f is given by .
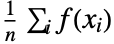  • For a continuous distribution dist, the expected value of f is given by 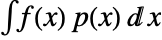where 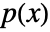is the probability density function of dist and the integral is taken over the domain of dist.
  • For a discrete distribution dist, the expected value of f is given by 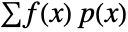where 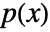is the probability mass function of dist and summation is over the domain of dist.
  • The following option can be given:
  • Assumptions $Assumptionsassumptions to make about parameters

Examples

open allclose all

Basic Examples  (3)

Find the expected value of in a Poisson distribution:

Use a pure function:

Expected value for a list:

Scope  (3)

Compute the expected value of any function:

Do the computation numerically:

Obtain expectations with conditions:

Options  (1)

Assumptions  (1)

Obtain results correct for given assumptions on symbols:

Applications  (2)

Obtain the raw moments of a distribution:

Construct a mixture density, here a Poisson‐inverse Gaussian mixture:

Properties & Relations  (7)

ExpectedValue of a function is the integral or sum of that function times the PDF:

ExpectedValue of for real t is the CharacteristicFunction:

ExpectedValue of a constant is the constant:

ExpectedValue of a random variable is the Mean:

ExpectedValue of the squared difference from the Mean is the Variance:

ExpectedValue for a list is a Mean:

CentralMoment is equivalent to an expected value:

Wolfram Research (2007), ExpectedValue, Wolfram Language function, https://reference.wolfram.com/language/ref/ExpectedValue.html (updated 2008).

Text

Wolfram Research (2007), ExpectedValue, Wolfram Language function, https://reference.wolfram.com/language/ref/ExpectedValue.html (updated 2008).

CMS

Wolfram Language. 2007. "ExpectedValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2008. https://reference.wolfram.com/language/ref/ExpectedValue.html.

APA

Wolfram Language. (2007). ExpectedValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ExpectedValue.html

BibTeX

@misc{reference.wolfram_2025_expectedvalue, author="Wolfram Research", title="{ExpectedValue}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/ExpectedValue.html}", note=[Accessed: 18-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_expectedvalue, organization={Wolfram Research}, title={ExpectedValue}, year={2008}, url={https://reference.wolfram.com/language/ref/ExpectedValue.html}, note=[Accessed: 18-April-2025 ]}