

Skewness
Details


- Skewness measures the asymmetry in data or of dist.
- Skewness[…] is equivalent to CentralMoment[…,3]/CentralMoment[…,2]3/2.
- A positive skewness
 indicates a distribution with a long right tail. A negative skewness indicates a distribution with a long left tail.
indicates a distribution with a long right tail. A negative skewness indicates a distribution with a long left tail. -
- Skewness[{{x1,y1,…},{x2,y2,…},…}] gives {Skewness[{x1,x2,…}],Skewness[{y1,y2,…}],…}.
- Skewness handles both numerical and symbolic data.
- The data can have the following additional forms and interpretations:
-
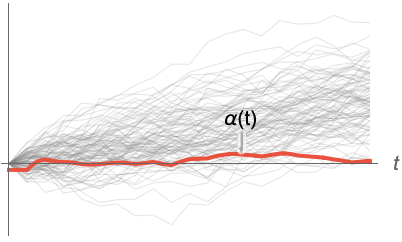
Association the values (the keys are ignored) » SparseArray as an array, equivalent to Normal[data] » QuantityArray quantities as an array » WeightedData weighted mean, based on the underlying EmpiricalDistribution » EventData based on the underlying SurvivalDistribution » TimeSeries, TemporalData, … vector or array of values (the time stamps ignored) » Image,Image3D RGB channel's values or grayscale intensity value » Audio amplitude values of all channels » DateObject, TimeObject list of dates or list of times » - For a random process proc, the skewness function can be computed for slice distribution at time t, SliceDistribution[proc,t], as α[t]=Skewness[SliceDistribution[proc,t]]. »
-
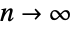
Examples
open all close allBasic Examples (4)
Scope (23)
Basic Uses (7)
Exact input yields exact output:
Approximate input yields approximate output:
Find the skewness of WeightedData:
Find the skewness of EventData:
Find the skewness of TemporalData:
Find the skewness of TimeSeries:
Array Data (5)
Skewness for a matrix gives columnwise skewness:
When the input is an Association, Skewness works on its values:
SparseArray data can be used just like dense arrays:
Find the skewness of a QuantityArray:
Image and Audio Data (2)
Channelwise skewness value of an RGB image:
Skewness intensity value of a grayscale image:
On audio objects, Skewness works channelwise:
Date and Time (5)
Applications (8)
Zero skewness indicates that the distribution is symmetric:
Distributions with longer tails to the right have positive skewness:
Distributions with longer tails to the left have negative skewness:
The limiting distribution for BinomialDistribution as ![]() is normal:
is normal:
The limiting value of skewness is 0:
By the central limit theorem, skewness of normalized sums of random variables will converge to 0:
Define a Pearson distribution with zero mean and unit variance, parameterized by skewness and kurtosis:
Obtain parameter inequalities for Pearson types 1, 4, and 6:
The region plot for Pearson types depending on the values of skewness and kurtosis:
Generate a random sample from a ParetoDistribution:
Determine the type of PearsonDistribution with moments matching the sample moments:
This time series contains the number of steps taken daily by a person during a period of five months:
Analyze the skewness as an indication of a tail in the daily step distribution:
The histogram of the frequency of daily counts confirms that the distribution has a longer left tail:
Find the skewness for the heights of children in a class:
Skewness close to 0 indicates distribution symmetric around the mean:
Properties & Relations (2)
Skewness for data can be computed from CentralMoment:
Skewness for a distribution can be computed from CentralMoment:
Possible Issues (1)
Neat Examples (1)
The distribution of Skewness estimates for 50, 100, and 300 samples:
See Also
Tech Notes
Text
Wolfram Research (2007), Skewness, Wolfram Language function, https://reference.wolfram.com/language/ref/Skewness.html (updated 2024).
CMS
Wolfram Language. 2007. "Skewness." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Skewness.html.
APA
Wolfram Language. (2007). Skewness. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Skewness.html
BibTeX
@misc{reference.wolfram_2025_skewness, author="Wolfram Research", title="{Skewness}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Skewness.html}", note=[Accessed: 21-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_skewness, organization={Wolfram Research}, title={Skewness}, year={2024}, url={https://reference.wolfram.com/language/ref/Skewness.html}, note=[Accessed: 21-February-2026]}