ExpectedValue

ExpectedValueはバージョン8.0でExpectationおよびNExpectationに置き換えられた．

ExpectedValue[f,list]

リスト list 中の値について純関数 f の期待値を与える．

ExpectedValue[f,list,x]

list の値についての x の関数 f の期待値を与える．

ExpectedValue[f,dist]

記号分布 dist についての純関数 f の期待値を与える．

ExpectedValue[f,dist,x]

記号分布 dist についての x の関数 f の期待値を与える．

詳細とオプション

  • リスト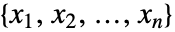についての f の期待値は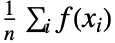で与えられる．
  • 連続分布 dist について，f の期待値は 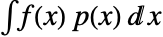で与えられる．ただし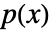，は dist の確率密度関数であり，積分は dist の領域で行われる．
  • 離散分布 dist について，f の期待値は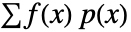で与えられる．ただし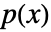，は dist の確率質量関数であり，総和は dist の領域で出される．
  • 次のオプションが使える．
  • Assumptions $Assumptionsパラメータについての仮定

例題

すべて開くすべて閉じる

例  (3)

ポアソン(Poisson)分布における の期待値を求める：

純関数を使う：

リストの予測される値：

スコープ  (3)

任意の関数の期待値を計算する：

数値的に計算する：

条件付きの期待値を求める：

オプション  (1)

Assumptions  (1)

与えられた記号に関する仮定について正しい結果を求める：

アプリケーション  (2)

分布の原点の周りのモーメントを求める：

混合密度，ここではポアソン・逆ガウス(Gauss)密度を構築する：

特性と関係  (7)

関数のExpectedValueは，その関数にPDFを掛けたものの総和または積分である：

実数 t についての のExpectedValueはCharacteristicFunctionである：

定数のExpectedValueは定数である：

ランダム変数のExpectedValueはMeanである：

Meanからの自乗差のExpectedValueはVarianceである：

リストのExpectedValueはMeanである：

CentralMomentは予測される値に等しい：

Wolfram Research (2007), ExpectedValue, Wolfram言語関数， https://reference.wolfram.com/language/ref/ExpectedValue.html （2008年に更新）.

テキスト

Wolfram Research (2007), ExpectedValue, Wolfram言語関数， https://reference.wolfram.com/language/ref/ExpectedValue.html （2008年に更新）.

CMS

Wolfram Language. 2007. "ExpectedValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2008. https://reference.wolfram.com/language/ref/ExpectedValue.html.

APA

Wolfram Language. (2007). ExpectedValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ExpectedValue.html

BibTeX

@misc{reference.wolfram_2024_expectedvalue, author="Wolfram Research", title="{ExpectedValue}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/ExpectedValue.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_expectedvalue, organization={Wolfram Research}, title={ExpectedValue}, year={2008}, url={https://reference.wolfram.com/language/ref/ExpectedValue.html}, note=[Accessed: 18-November-2024 ]}