n!
n の階乗を与える.




Factorial 
n!
n の階乗を与える.
予備知識
- Factorialは階乗関数を表す.具体的に言うと,Factorial[n]は与えられた数
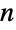 の階乗
の階乗 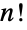 を返す.これは,正の整数については,
を返す.これは,正の整数については,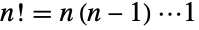 と定義される.n1,2,…の最初のいくつかの値は1,2,6,24,120,720,…となる.特殊ケースの
と定義される.n1,2,…の最初のいくつかの値は1,2,6,24,120,720,…となる.特殊ケースの 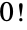 は1と定義される.この定義は,0個のオブジェクトを並べる方法は厳密に1通りであるという組合せ論の解釈と矛盾しない.一般的な複素数
は1と定義される.この定義は,0個のオブジェクトを並べる方法は厳密に1通りであるという組合せ論の解釈と矛盾しない.一般的な複素数 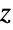 については,
については,![z!=TemplateBox[{{z, +, 1}}, Gamma] z!=TemplateBox[{{z, +, 1}}, Gamma]](Files/Factorial.ja/6.png) となる.ここに含まれるGamma関数
となる.ここに含まれるGamma関数 ![TemplateBox[{z}, Gamma] TemplateBox[{z}, Gamma]](Files/Factorial.ja/7.png) は,
は,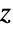 が負の整数である場合(この場合の
が負の整数である場合(この場合の 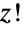 は複素無限大となる)を除く,
は複素無限大となる)を除く,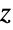 のすべての複素値について,
のすべての複素値について,![TemplateBox[{z}, Gamma]=int_0^inftyⅇ^(-t) t^(z-1)dt TemplateBox[{z}, Gamma]=int_0^inftyⅇ^(-t) t^(z-1)dt](Files/Factorial.ja/11.png) と定義される.半整数の階乗は
と定義される.半整数の階乗は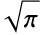 の有理数倍で表される.
の有理数倍で表される. - 階乗は,置換として知られる,リストの元の一定の順序への並べ替えを数える場合がよく知られている.置換はPermutationsで生成することができる.相異なる
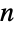 個の元のリストには
個の元のリストには 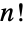 通りの置換がある.これは,最初の元が置ける場所は
通りの置換がある.これは,最初の元が置ける場所は 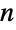 個,最初の元の場所が決まった後で2番目の元が置ける場所は
個,最初の元の場所が決まった後で2番目の元が置ける場所は 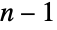 個,最初の2個の元の場所が決まった後で3番目の元が置ける場所は
個,最初の2個の元の場所が決まった後で3番目の元が置ける場所は 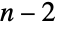 個と言う具合にして,最後に残った場所に最後に残った元を置くまで続ける.これに従うと,
個と言う具合にして,最後に残った場所に最後に残った元を置くまで続ける.これに従うと,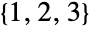 の置換は
の置換は 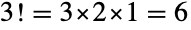 通りで,
通りで,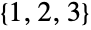 ,
,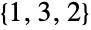 ,
,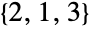 ,
,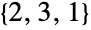 ,
,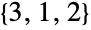 ,
,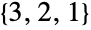 となる.
となる. - より一般的に言うと,相異なる
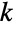 個の元(
個の元(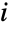 番目の元は
番目の元は 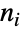 個のコピーを持つ)の
個のコピーを持つ)の 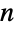 個の多重集合(したがって,
個の多重集合(したがって,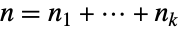 )の置換数は,Multinomialが与える多項係数
)の置換数は,Multinomialが与える多項係数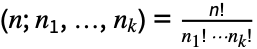 に等しい.多項係数
に等しい.多項係数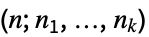 もまた,
もまた,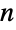 個の元を,大きさが n1,…,nkのラベル付きの
個の元を,大きさが n1,…,nkのラベル付きの 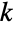 個の部分集合に分割する方法を数える.これは,Binomialが与える二項係数
個の部分集合に分割する方法を数える.これは,Binomialが与える二項係数![TemplateBox[{n, m}, Binomial] TemplateBox[{n, m}, Binomial]](Files/Factorial.ja/36.png) と同じで,
と同じで,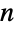 元の集合の
元の集合の 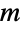 元部分集合を数えると定義され,
元部分集合を数えると定義され,![TemplateBox[{n, m}, Binomial]=(n;m,n-m)=(n!)/(m! (n-m)!) TemplateBox[{n, m}, Binomial]=(n;m,n-m)=(n!)/(m! (n-m)!)](Files/Factorial.ja/39.png) を満足する.
を満足する. - 階乗関数は,再帰関数
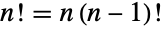 および
および 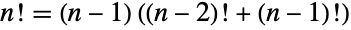 を満足する.階乗関数は,スターリング(Stirling)の近似
を満足する.階乗関数は,スターリング(Stirling)の近似 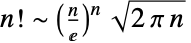 が示すように,他のどの指数関数よりも急激に増大する.階乗は整数論とその解析の基本的な結果にも出現する.ウィルソン(Wilson)の定理には,
が示すように,他のどの指数関数よりも急激に増大する.階乗は整数論とその解析の基本的な結果にも出現する.ウィルソン(Wilson)の定理には,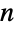 が素数のときかつそのときに限り
が素数のときかつそのときに限り![TemplateBox[{{{{(, {n, -, 1}, )}, !}, =, {-, 1}}, n}, Mod] TemplateBox[{{{{(, {n, -, 1}, )}, !}, =, {-, 1}}, n}, Mod]](Files/Factorial.ja/44.png) ,とある.
,とある.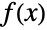 が無限に微分可能なスカラー関数であれば,点
が無限に微分可能なスカラー関数であれば,点 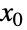 (Seriesで計算可)の周りのテイラー(Taylor)級数表現は
(Seriesで計算可)の周りのテイラー(Taylor)級数表現は 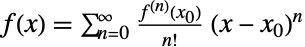 で与えられる.指数関数
で与えられる.指数関数 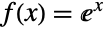 のテイラー級数で
のテイラー級数で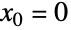 および
および 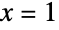 と設定すると,E(自然対数の底)についての美しい恒等式
と設定すると,E(自然対数の底)についての美しい恒等式 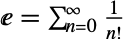 が与えられる.
が与えられる. - Factorialと関連がある,あるいはこれの一般化である関数には,Factorial2,FactorialPower,
![TemplateBox[{Subfactorial, paclet:ref/Subfactorial}, RefLink, BaseStyle -> {InlineFormula}] TemplateBox[{Subfactorial, paclet:ref/Subfactorial}, RefLink, BaseStyle -> {InlineFormula}]](Files/Factorial.ja/52.png) ,QFactorial,BarnesG,Pochhammerがある.
,QFactorial,BarnesG,Pochhammerがある.
例題
すべて開く すべて閉じる例 (7)
Infinityにおける級数展開:
スコープ (34)
数値評価 (6)
IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する:
Aroundを使って平均的な場合の統計区間を計算することもできる:
MatrixFunctionを使って行列のFactorial関数を計算することもできる:
可視化 (2)
関数の特性 (10)
級数展開 (5)
関数表現 (2)
一般化と拡張 (4)
アプリケーション (6)
複素平面におけるFactorialの絶対値のプロット:
特性と関係 (9)
FullSimplifyを使ってFactorialを含む式を簡約する:
Factorialを含む母関数の総和を計算する:
Factorialを含む数値的な総和を計算する:
FactorialはDifferenceRootとして表すことができる:
FindSequenceFunctionはFactorial数列を認識する:
Factorialの指数母関数:
おもしろい例題 (3)
関連項目
Gamma Binomial Pochhammer Factorial2 FactorialPower Subfactorial QFactorial
Function Repository: KurepaK MultiFactorial Primorial FactorialMod TripleGamma
テクニカルノート
-
▪
- 数学関数 ▪
- 組合せ関数 ▪
- 実装に関するノート:数値および関連関数
関連するガイド
-
▪
- 組合せ関数 ▪
- 離散数学 ▪
- 再帰関数と総和関数 ▪
- 数学関数 ▪
- 整数関数 ▪
- ガンマ関数と関連関数 ▪
- 整数列 ▪
- 統計学で使用される関数
履歴
1988 で導入 (1.0) | 2021 で更新 (13.0) ▪ 2022 (13.1)
テキスト
Wolfram Research (1988), Factorial, Wolfram言語関数, https://reference.wolfram.com/language/ref/Factorial.html (2022年に更新).
CMS
Wolfram Language. 1988. "Factorial." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/Factorial.html.
APA
Wolfram Language. (1988). Factorial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Factorial.html
BibTeX
@misc{reference.wolfram_2025_factorial, author="Wolfram Research", title="{Factorial}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/Factorial.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_factorial, organization={Wolfram Research}, title={Factorial}, year={2022}, url={https://reference.wolfram.com/language/ref/Factorial.html}, note=[Accessed: 05-February-2026]}