Factorial 
n!
给出 n 的阶乘.
背景
- Factorial 表示阶乘函数. 具体来讲,Factorial[n] 返回给定数字
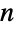 的阶乘
的阶乘 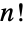 ,对于正整数,其定义为
,对于正整数,其定义为 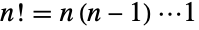 . 对于 n1,2,…,前几个值为 1,2,6,24,120,720,…. 特殊情况
. 对于 n1,2,…,前几个值为 1,2,6,24,120,720,…. 特殊情况 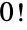 被定义为 1,与排列组合的解释一致,正好只有一种排列零个对象的方法. 对于一般复数
被定义为 1,与排列组合的解释一致,正好只有一种排列零个对象的方法. 对于一般复数 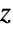 ,
,![z!=TemplateBox[{{z, +, 1}}, Gamma] z!=TemplateBox[{{z, +, 1}}, Gamma]](Files/Factorial.zh/6.png) ,其中 Gamma 函数
,其中 Gamma 函数 ![TemplateBox[{z}, Gamma] TemplateBox[{z}, Gamma]](Files/Factorial.zh/7.png) 的定义为
的定义为 ![TemplateBox[{z}, Gamma]=int_0^inftyⅇ^(-t) t^(z-1)dt TemplateBox[{z}, Gamma]=int_0^inftyⅇ^(-t) t^(z-1)dt](Files/Factorial.zh/8.png) ,该定义对所有复数
,该定义对所有复数 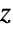 成立,除了
成立,除了 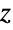 是负整数的情况(这时
是负整数的情况(这时 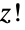 为负无穷). 半整数的阶乘由
为负无穷). 半整数的阶乘由 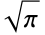 的有理倍数给出.
的有理倍数给出. - 最为大家熟知的是阶乘可以计算列表元素固定排序的数量,称为置换,可用 Permutations 生成. 对于由
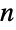 个(不同的)元素组成的列表,有
个(不同的)元素组成的列表,有 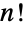 种置换,原因是有
种置换,原因是有 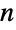 个位置可以放置第一个元素,第一个元素放好后,有
个位置可以放置第一个元素,第一个元素放好后,有 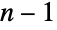 个位置可以放置第二个元素,前两个元素放好后,有
个位置可以放置第二个元素,前两个元素放好后,有 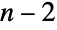 个位置可以放置第三个元素,以此类推,直到只剩下一个位置,可以放置最后一个元素. 因此对于
个位置可以放置第三个元素,以此类推,直到只剩下一个位置,可以放置最后一个元素. 因此对于 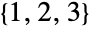 ,有
,有 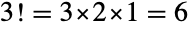 种置换,即
种置换,即 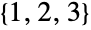 、
、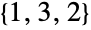 、
、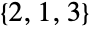 、
、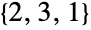 、
、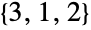 和
和 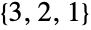 .
. - 更广泛地说,对于
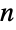 个元素的多重集合 (multiset), 其中有
个元素的多重集合 (multiset), 其中有 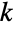 个不同的元素,第
个不同的元素,第 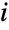
 个不同的元素有
个不同的元素有 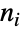 份拷贝(因此
份拷贝(因此 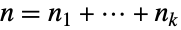 ),置换的数量等于由 Multinomial 给出的多项式系数
),置换的数量等于由 Multinomial 给出的多项式系数 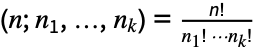 . 多项式系数
. 多项式系数 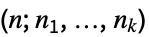 也可以计算将
也可以计算将 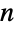 个元素的集合划分成
个元素的集合划分成 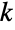 个有标签的、大小为 n1,…,nk 的子集的方法的数量. 因此由 Binomial 给出的二项式系数
个有标签的、大小为 n1,…,nk 的子集的方法的数量. 因此由 Binomial 给出的二项式系数 ![TemplateBox[{n, m}, Binomial] TemplateBox[{n, m}, Binomial]](Files/Factorial.zh/37.png) 被定义为计算
被定义为计算 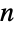 个元素组成的集合的
个元素组成的集合的 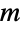 个元素的子集的数量,它满足
个元素的子集的数量,它满足 ![TemplateBox[{n, m}, Binomial]=(n;m,n-m)=(n!)/(m! (n-m)!) TemplateBox[{n, m}, Binomial]=(n;m,n-m)=(n!)/(m! (n-m)!)](Files/Factorial.zh/40.png) .
. - 阶乘函数满足循环关系式
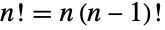 和
和 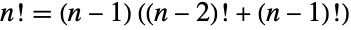 . 它比所有指数函数增长得都快,从 Stirling 逼近
. 它比所有指数函数增长得都快,从 Stirling 逼近 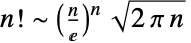 可以看出. 阶乘也出现在数论和分析的基本结果中. Wilson 定理指出
可以看出. 阶乘也出现在数论和分析的基本结果中. Wilson 定理指出 ![TemplateBox[{{{{(, {n, -, 1}, )}, !}, =, {-, 1}}, n}, Mod] TemplateBox[{{{{(, {n, -, 1}, )}, !}, =, {-, 1}}, n}, Mod]](Files/Factorial.zh/44.png) ,当且仅当
,当且仅当 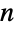 为质数时. 如果
为质数时. 如果 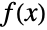 是一个无限可微的标量函数,则其关于点
是一个无限可微的标量函数,则其关于点 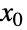 (可用 Series 算出)的泰勒级数表示由
(可用 Series 算出)的泰勒级数表示由 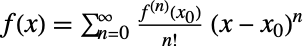 给出. 在指数函数
给出. 在指数函数 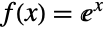 的泰勒级数中设置
的泰勒级数中设置 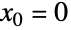 和
和 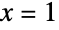 给出了完美的 E(自然对数的底数)的恒等式
给出了完美的 E(自然对数的底数)的恒等式 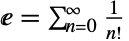 .
. - 其他与 Factorial 有关的函数或拓展 Factorial 的函数包括 Factorial2、 FactorialPower、
![TemplateBox[{Subfactorial, paclet:ref/Subfactorial}, RefLink, BaseStyle -> {InlineFormula}] TemplateBox[{Subfactorial, paclet:ref/Subfactorial}, RefLink, BaseStyle -> {InlineFormula}]](Files/Factorial.zh/53.png) 、QFactorial、BarnesG 和 Pochhammer.
、QFactorial、BarnesG 和 Pochhammer.
范例
打开所有单元关闭所有单元基本范例 (7)
范围 (34)
数值计算 (6)
用 Interval 和 CenteredInterval 对象计算最坏情况下的区间:
或用 Around 计算普通的统计区间:
或者用 MatrixFunction 计算矩阵形式的 Factorial 函数::
可视化 (2)
函数属性 (10)
级数展开 (5)
函数表示 (2)
推广和延伸 (4)
应用 (6)
在复平面上绘制 Factorial 的绝对值:
属性和关系 (9)
用 FullSimplify 来化简包含 Factorial 的表达式:
计算涉及 Factorial 生成函数的和:
计算涉及 Factorial 的数值和:
Factorial 可被表示为 DifferenceRoot:
FindSequenceFunction 可以识别 Factorial 序列:
Factorial 的指数母函数:
巧妙范例 (3)
Wolfram Research (1988),Factorial,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Factorial.html (更新于 2022 年).
文本
Wolfram Research (1988),Factorial,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Factorial.html (更新于 2022 年).
CMS
Wolfram 语言. 1988. "Factorial." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2022. https://reference.wolfram.com/language/ref/Factorial.html.
APA
Wolfram 语言. (1988). Factorial. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Factorial.html 年