FactorialMoment
FactorialMoment[data,r]
data の r![]() 次階乗モーメント
次階乗モーメント ![]() を与える.
を与える.
FactorialMoment[data,{r1,…,rm}]
data の多変量{r1,…,rm}次階乗モーメント ![]() を与える.
を与える.
FactorialMoment[dist,…]
分布 dist の階乗モーメントを与える.
r![]() 次の形式的階乗モーメントを表す.
次の形式的階乗モーメントを表す.
詳細


- 階乗モーメントは,
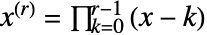 によって与えられるFactorialPower[x,r]を使って定義される.
によって与えられるFactorialPower[x,r]を使って定義される. - 次数 r のスカラーで data が配列
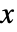 のとき:
のとき: -
![x in TemplateBox[{Vectors, paclet:ref/Vectors}, RefLink, BaseStyle -> {3ColumnTableMod}][n] x in TemplateBox[{Vectors, paclet:ref/Vectors}, RefLink, BaseStyle -> {3ColumnTableMod}][n]](Files/FactorialMoment.ja/8.png)
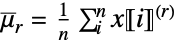
r 次階乗ベキの和 » ![x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}] x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}]](Files/FactorialMoment.ja/10.png)
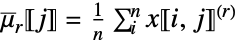
列ごとの r 次階乗ベキの和 » ![x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}] x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}]](Files/FactorialMoment.ja/12.png)
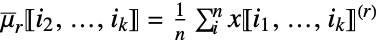
列ごとの r 次階乗ベキの和 » - FactorialMoment[x,r]はArrayReduce[FactorialMoment[#,r]&,x,1]に等しい.
- 次数{r1,…,rm}のベクトルで data が配列
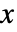 のとき:
のとき: -
![x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}] x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}]](Files/FactorialMoment.ja/15.png)
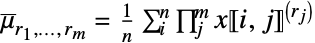
第 j 列の rj次階乗ベキの和 ![x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}] x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}]](Files/FactorialMoment.ja/17.png)
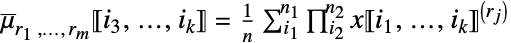
第 j 列の rj次階乗ベキの和 » - FactorialMoment[x,{r1,…,rm}]はArrayReduce[FactorialMoment[#,{r1,…,rm}]&,x,{{1},{2}}]に等しい.
- FactorialMomentは数値データと記号データの両方を扱うことができる.
- data は次の追加的な形式と解釈を持つことができる.
-
Association 値(キーは無視される) » WeightedData もとになっているEmpiricalDistributionに基づく加重平均 » EventData もとになっているSurvivalDistributionに基づく » TimeSeries, TemporalData, … 値のベクトルまたは配列(タイムスタンプは無視される) » Image,Image3D RGBチャンネル値またはグレースケール強度値 » Audio すべてのチャンネルの振幅値 » - 分布 dist についての r
 次階乗モーメントは Expectation[x(r),xdist]で与えられる. »
次階乗モーメントは Expectation[x(r),xdist]で与えられる. » - 多変量分布 dist についての{r1,…,rm}
 次階乗モーメントはExpectation[x1(r1)⋯ xm(rm),{x1,…,xm}dist]で与えられる. »
次階乗モーメントはExpectation[x1(r1)⋯ xm(rm),{x1,…,xm}dist]で与えられる. » - ランダム過程 proc については,階乗モーメント関数は時点 t におけるスライス分布SliceDistribution[proc,t]について,
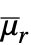 [t]=FactorialMoment[SliceDistribution[proc,t],r]として計算できる. »
[t]=FactorialMoment[SliceDistribution[proc,t],r]として計算できる. » - FactorialMoment[r]はMomentConvertやMomentEvaluate等の関数で使うことができる. »
例題
すべて開くすべて閉じるスコープ (20)
基本的な用法 (5)
配列データ (4)
FactorialMomentは,行列については列ごとの平均を与える:
FactorialMomentは,配列については第1レベルの列ごとの平均を与える:
配列についての多変量FactorialMoment:
入力がAssociationのとき,FactorialMomentはその値に作用する:
SparseArrayデータは密は配列のように使うことができる:
画像データと音声データ (2)
分布のモーメントと過程のモーメント (5)
階乗モーメントは特定の次数についてしか評価されないことがある:
ある時点 t=0.5におけるTemporalDataの階乗モーメントを求める:
形式的なモーメント (4)
形式的なモーメントのTraditionalFormによる表示:
形式的なモーメントの組合せを,FactorialMomentを含む式に変換する:
FactorialMomentを含む式についてのサンプル推定量を求める:
アプリケーション (4)
特性と関係 (5)
階乗モーメント ![]() はFactorialPowerの期待値と等しい:
はFactorialPowerの期待値と等しい:
一次階乗モーメントはMeanと等しい:
FactorialMomentは ![]() を使ってMomentから計算することができる:
を使ってMomentから計算することができる:
MomentConvertも同じ結果を生む:
Momentは ![]() を使ってFactorialMomentから計算することができる:
を使ってFactorialMomentから計算することができる:
MomentConvertも同じ結果を生む:
おもしろい例題 (1)
30個,100個,300個のサンプルについてFactorialMomentの分布を推定する:
テキスト
Wolfram Research (2010), FactorialMoment, Wolfram言語関数, https://reference.wolfram.com/language/ref/FactorialMoment.html (2024年に更新).
CMS
Wolfram Language. 2010. "FactorialMoment." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/FactorialMoment.html.
APA
Wolfram Language. (2010). FactorialMoment. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FactorialMoment.html