WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

FourierSinTransform

FourierSinTransform[expr,t,ω]

expr の記号フーリエ正弦変換を与える．

FourierSinTransform[expr,{t₁,t₂,…},{ω₁,ω₂,…}]

expr の多次元正弦フーリエ変換を与える．

詳細とオプション

関数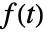のフーリエ正弦変換はデフォルトでは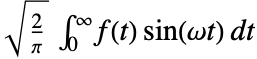で定義される．
関数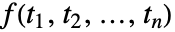の多次元フーリエ正弦変換は，デフォルトで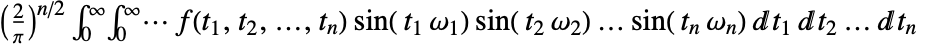，と定義される．
理工学では他の定義が使用されることもある．
別の定義はオプションFourierParametersを使用して指定できる．
と設定すると，FourierSinTransformで計算されるフーリエ正弦変換は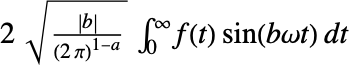となる．
AssumptionsおよびIntegrateの他のオプションもFourierSinTransformで使うことができる．

例題

すべて開くすべて閉じる

例 (3)

スコープ (5)

初等関数：

特殊関数：

一般化された関数：

周期関数：

多変数変換：

オプション (3)

Assumptions (1)

BesselJのフーリエ正弦変換は区分関数である：

FourierParameters (1)

FourierParametersのデフォルトの設定値は{0,1}である：

変換の異なる定義にデフォルト以外の設定値を使う：

逆変換にも同じFourierParametersの設定値を使う：

GenerateConditions (1)

GenerateConditions->Trueを使って結果が有効となる場合に必要なパラメータ条件を得る：

特性と関係 (3)

Asymptoticを使って漸近近似を計算する：

FourierSinTransformとInverseFourierSinTransform は互いに逆関数である：

FourierSinTransformとFourierTransformの結果は，奇関数についてはIという因数の分だけ異なる：

結果は ω>0についてはIの分だけ異なる：

考えられる問題 (1)

フーリエ正弦変換はDiracDelta等の一般化された関数によって与えられることがある：

おもしろい例題 (1)

MeijerGによって表現されたフーリエ正弦変換：

トップへ