Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

FourierSinTransform

FourierSinTransform[expr,t,ω]

给出 expr 的符号傅立叶正弦变换.

FourierSinTransform[expr,{t₁,t₂,…},{ω₁,ω₂,…}]

给出 expr 的多维傅立叶正弦变换.

更多信息和选项

函数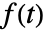的傅立叶正弦变换缺省情况下定义为 .
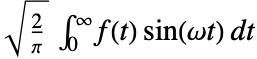缺省情况下，函数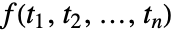的多维傅立叶正弦变换被定义为 .
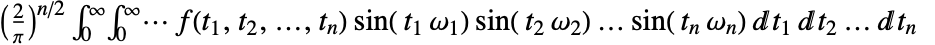其它定义用在一些科学和技术领域中.
选择不同的定义可以用选项 FourierParameters 指定.
设置下，由 FourierSinTransform 计算的傅立叶正弦变换是 .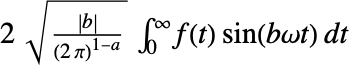
Assumptions 和其它 Integrate 的选项同样可以在 FourierSinTransform 中给出.

范例

打开所有单元关闭所有单元

基本范例 (3)

范围 (5)

初等函数：

特殊函数：

广义函数：

周期函数：

多元变换：

选项 (3)

Assumptions (1)

BesselJ 的傅立叶正弦变换是一个分段函数：

FourierParameters (1)

FourierParameters 的缺省设置是 {0,1}：

对不同定义的变换用非缺省设置：

为了获得逆，用相同的 FourierParameters 设置：

GenerateConditions (1)

当结果有效时，用 GenerateConditions->True 来获得参数条件：

属性和关系 (3)

用 Asymptotic 计算渐近逼近：

FourierSinTransform 和 InverseFourierSinTransform 是互逆的：

对于奇函数，从 FourierSinTransform 和 FourierTransform 中获得的结果差一个 I 因子：

对 ω>0 结果相差一个 I 因子：

可能存在的问题 (1)

傅立叶正弦函数可能会按广义函数给出，例如 DiracDelta：

巧妙范例 (1)

用 MeijerG 表示傅立叶正弦变换：

顶部