Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

FoxH

FoxH[{{{a₁,α₁},…,{a_n,α_n}},{{a_n+1,α_n+1},…,{a_p,α_p}}},{{{b₁,β₁},…,{b_m,β_m}},{{b_m+1,β_m+1},…,{b_q,β_q}}},z]

is the Fox H-function .

Details

Mathematical function, suitable for both symbolic and numerical manipulation.
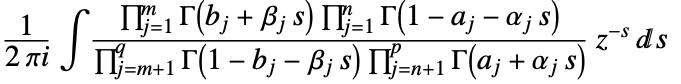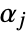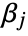FoxH generalizes the MeijerG function and is defined by the Mellin–Barnes integral where and are positive real numbers and the integration is along a path 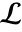separating the poles of 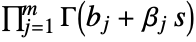from the poles of .
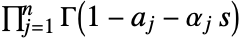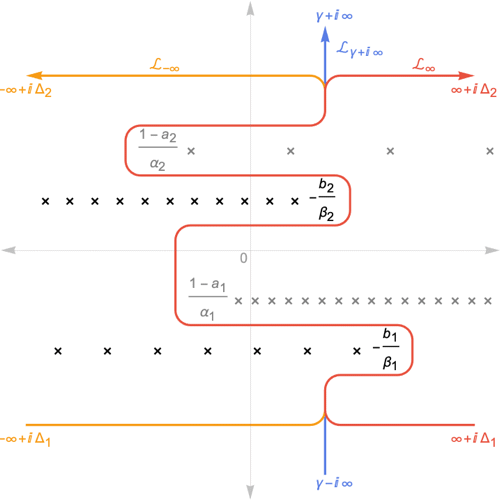
Three choices are possible for the path :
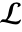a.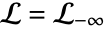 is a loop beginning at 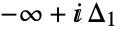and ending at 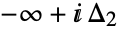and encircling all the poles of 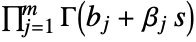once in the positive direction.
b.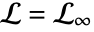 is a loop beginning at 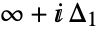and ending at 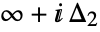and encircling all the poles of 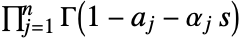once in the negative direction.
c.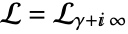 is a contour starting at the point 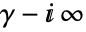and going to 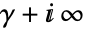such that all the poles of 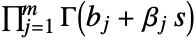are separated from the poles of .

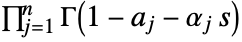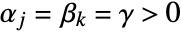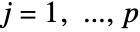FoxH specializes to MeijerG if for and : .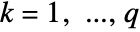
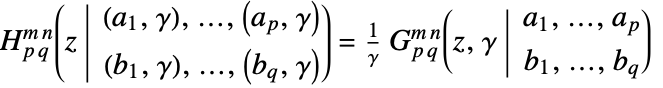In many special cases, FoxH is automatically converted to other functions.
FoxH can be evaluated for arbitrary complex parameters.
FoxH can be evaluated to arbitrary numerical precision.
FoxH automatically threads over lists. »

Examples

open allclose all

Basic Examples (6)

Evaluate numerically:

Many special functions are special cases of FoxH:

Some cases cannot be easily expressed in terms of MeijerG:

Plot the FoxH function:

Plot over a subset of the complexes:

Series expansion at the origin:

Leading asymptotic term at Infinity:

Scope (28)

Numerical Evaluation (7)

Evaluate to high precision:

The precision of the output tracks the precision of the input:

FoxH takes complex number parameters and :

FoxH takes complex number arguments:

Evaluate FoxH efficiently at high precision:

Compute the elementwise values of an array using automatic threading:

Or compute the matrix FoxH function using MatrixFunction:

Compute average-case statistical intervals using Around:

Specific Values (3)

Values at fixed points:

Evaluate FoxH symbolically:

Values at zero:

Visualization (4)

Plot a family of FoxH functions:

ComplexContourPlot of FoxH[{{{},{}},{{{-1,1/2}},{}}, z]:

Use AbsArgPlot and ReImPlot to plot complex values of FoxH over the real numbers:

Plot FoxH as a function of parameters and :

Function Properties (5)

For simple parameters, FoxH evaluates to simpler functions:

FoxH is symmetric in the pairs and :

FoxH might reduce to a simpler FoxH if some of the pairs are equal:

A more complex case:

FoxH threads elementwise over lists in the last argument:

TraditionalForm formatting:

Differentiation (2)

First derivative with respect to z:

Higher-order derivative with respect to z:

Formula for the derivative of a specific FoxH with respect to z:

Integration (3)

Compute the indefinite integral using Integrate:

Verify it by calculating the antiderivative:

Definite integral:

Some other integrals:

Series Expansions (4)

Get the series expansion of some FoxH function at the origin:

The first three approximations of this FoxH function around :

Plot these approximations:

Find the series expansion of a general FoxH function at the origin:

Find the series expansion of a general FoxH function at Infinity:

Get the general term in the series expansion using SeriesCoefficient:

Applications (3)

Use FoxHReduce to get the representation of almost any mathematical function in terms of FoxH:

More exotic combinations:

A root of the trinomial equation can be written in terms of FoxH:

Verify this for :

The roots of the general trinomial can also be expressed in terms of FoxH:

Verify these roots for and :

Express the PDF of StableDistribution in terms of FoxH for the case of :

Evaluate it and compare with the built-in PDF generated using StableDistribution:

Properties & Relations (2)

Use FunctionExpand to expand FoxH into simpler functions:

FoxHReduce returns FoxH representations of functions:

Possible Issues (3)

is a singular point of FoxH:

Series at the origin is available when the parameters are positive and are positive and exact:

Series at Infinity is available when the parameters are positive and are positive and exact:

Neat Examples (1)

Many elementary and special functions are special cases of FoxH:

Top