WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

FoxH

FoxH[{{{a₁,α₁},…,{a_n,α_n}},{{a_n+1,α_n+1},…,{a_p,α_p}}},{{{b₁,β₁},…,{b_m,β_m}},{{b_m+1,β_m+1},…,{b_q,β_q}}},z]

FoxのH関数である．

詳細

記号操作・数値操作の両方に適した数学関数である．
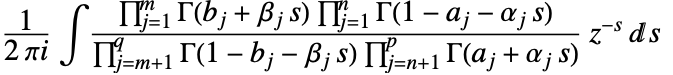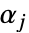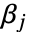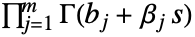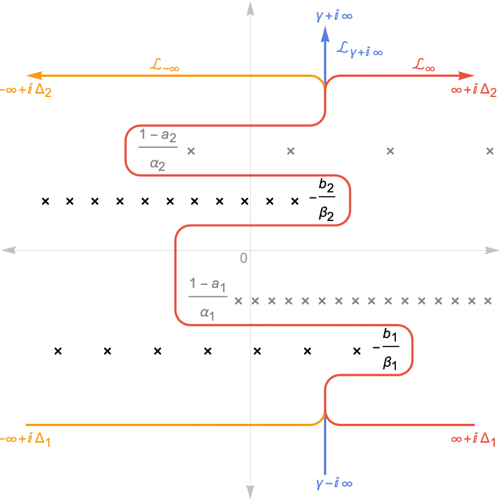
FoxHはMeijerG関数を一般化するもので，Mellin–Barnes積分で定義される．ただし，とは正の実数で積分はの極を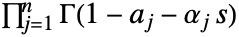の極から分割する経路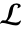に沿っている．
経路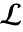には以下の3つの選択肢がある．
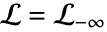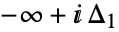a. はで始まって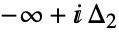で終るループで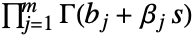，のすべての極を正の方向に一度取り囲む．
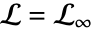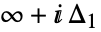b. はで始まって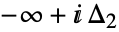で終るループで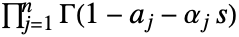，のすべての極を負の方向に一度取り囲む．
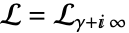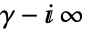c. は，始まり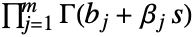，のすべての極が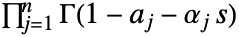の極から分離されるように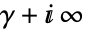へ向かう曲線である．

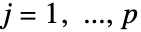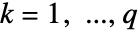およびについて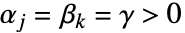なら， FoxHはMeijerGに特化されている．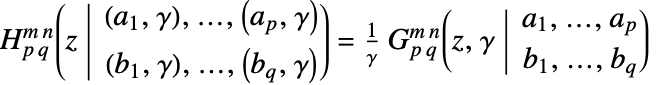
FoxHは，多くの特殊ケースで他の関数に自動的に変換される．
FoxHは任意の複素パラメータについて評価できる．
FoxHは任意の数値精度で評価できる．
FoxHは自動的にリストに縫い込まれる． »

例題

すべて開くすべて閉じる

例 (6)

数値的に解釈する：

特殊関数の多くはFoxHの特殊ケースである：

中にはMeijerGでは簡単には表せないものもある：

FoxH関数をプロットする：

複素数の部分集合上でプロットする：

原点における級数展開：

Infinityにおける最高次の漸近項：

スコープ (28)

数値評価 (7)

高精度で評価する：

出力精度は入力精度に従う：

FoxHは複素数パラメータのとを取る：

FoxHは複素引数を取る：

FoxHを高精度で効率的に評価する：

自動縫込みを使って配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のFoxH関数を計算することもできる：

Aroundを使って平均的な場合の統計区間を計算する：

特定の値 (3)

固定点における値：

FoxHを記号的に評価する：

零点における値：

可視化 (4)

FoxH関数族をプロットする：

FoxH[{{{},{}},{{{-1,1/2}},{}}, z]のComplexContourPlot：

AbsArgPlotとReImPlotを使ってFoxHの複素値を実数上にプロットする：

FoxHをパラメータおよびの関数としてプロットする：

関数の特性 (5)

FoxHは，単純なパラメータについて評価するとより簡単な関数になる：

FoxHはとのペアについて対称である：

FoxHは，ペアのいくつかが等しい場合は，より簡単なFoxHに簡約できるかもしれない：

より複雑なケース：

FoxHは要素単位で最後の引数のリストに縫い込まれる：

TraditionalFormによる表示：

微分 (2)

z についての一次導関数：

z についてのより高次の導関数：

z についての特定のFoxHの次導関数の式：

積分 (3)

Integrateを使って不定積分を計算する：

不定積分を計算することでこれを確かめる：

定積分：

その他の積分：

級数展開 (4)

原点におけるあるFoxH関数の級数展開を得る：

の周りのFoxH関数の最初の3つの近似：

これらの近似をプロットする：

原点における一般的なFoxH関数の級数展開を求める：

Infinityにおける一般的なFoxH関数の級数展開を求める：

SeriesCoefficientを使って級数展開の一般項を得る：

アプリケーション (3)

FoxHReduceを使ってほとんどすべての数学関数のFoxHによる表現を得る：

より珍しい組合せ：

三項式の根はFoxHによって書くことができる：

についてこれを確認する：

一般的な三項式の根もFoxHによって書くことができる：

これらの根をとについて確認する：

StableDistributionのPDFを，のときにFoxHによって表す：

評価してStableDistributionを使って生成された組込みのPDFと比較する：

特性と関係 (2)

FunctionExpandを使ってFoxHをより簡単な関数に展開する：

FoxHReduceは関数のFoxH表現を返す：

考えられる問題 (3)

はFoxHの特異点である：

原点におけるSeriesはパラメータが正でパラメータが正の厳密値のときにのみ得られる：

InfinityにおけるSeriesはパラメータおよびが正で後者が厳密値のときにのみ得られる：

おもしろい例題 (1)

初等関数および特殊関数の多くはFoxHの特殊ケースである：

トップへ