Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

FoxH

FoxH[{{{a₁,α₁},…,{a_n,α_n}},{{a_n+1,α_n+1},…,{a_p,α_p}}},{{{b₁,β₁},…,{b_m,β_m}},{{b_m+1,β_m+1},…,{b_q,β_q}}},z]

是 Fox H 函数 .

更多信息

数学函数，适用于符号和数值运算.
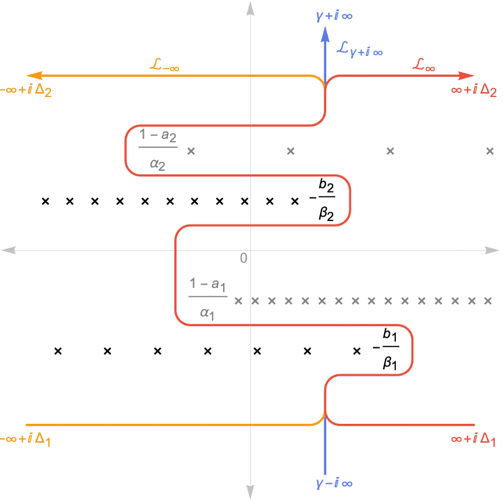
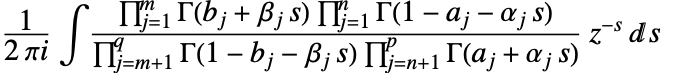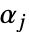FoxH 是 MeijerG 函数的推广，由 Mellin–Barnes 积分定义，其中和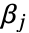为正实数，并且积分沿着将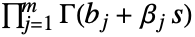的极点与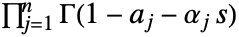的极点分开的路径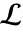进行.
路径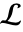可能有三种选择：
a.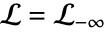 是一个环形，从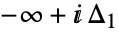开始，到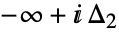结束，并沿正方向将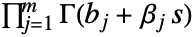的所有极点环绕一遍.
b.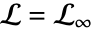 是一个环形，从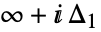开始，到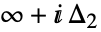结束，并沿负方向将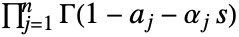的所有极点环绕一遍.
c.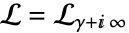 是一个从点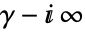开始到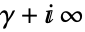的轮廓，使得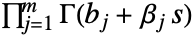的所有极点与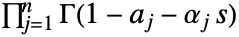的极点分开.

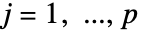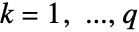如果对于和，有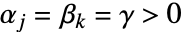成立，则 FoxH 即 MeijerG: .
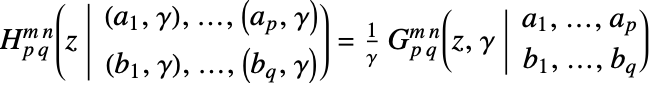在许多特殊情况下，FoxH 会自动转换为其他函数.
FoxH 可以对任意复数参数进行运算.
FoxH 可以求任意数值精度的值.
FoxH 自动遍历列表. »

范例

打开所有单元关闭所有单元

基本范例 (6)

数值运算：

许多特殊函数是 FoxH 的特例：

很多特例无法用 MeijerG 轻松表示：

绘制 FoxH 函数：

在复数子集上绘图：

原点处的级数展开：

Infinity 处的渐进首项：

范围 (28)

数值运算 (7)

运算值高精度：

输出的精度与输入的精度一致：

FoxH 接受复数参数和：

FoxH 接受复数自变量：

高精度高效运算 FoxH：

自动逐项计算数组中每个元素的值：

或用 MatrixFunction 计算矩阵形式的 FoxH 函数：

用 Around 计算一般情况下的统计区间：

特定值 (3)

在固定点的值：

符号式运算 FoxH：

在零点的值：

可视化 (4)

绘制一系列 FoxH 函数：

FoxH[{{{},{}},{{{-1,1/2}},{}}, z] 的 ComplexContourPlot：

使用 AbsArgPlot 和 ReImPlot 在实数上绘制 FoxH 的复数值：

将 FoxH 作为参数和的函数绘图：

函数属性 (5)

对于简单的参数，FoxH 运算为较简单的函数：

FoxH 在和数对中是对称的：

如果某些数对相等，FoxH 可能会简化为更简单的 FoxH：

更复杂的例子：

FoxH 在最后一个参数上按元素遍历列表：

TraditionalForm 格式化：

微分 (2)

关于 z 的一阶导数：

关于 z 的更高阶导数：

特定 FoxH 关于 z 的阶导数的公式：

积分 (3)

使用 Integrate 计算不定积分：

通过计算反导数进行验证：

定积分：

一些其他的积分：

级数展开 (4)

获取某些 FoxH 函数在原点处的级数展开：

该 FoxH 函数在附近的前三个近似：

绘制这些近似：

求一般 FoxH 函数在原点处的级数展开：

求一般 FoxH 函数在 Infinity 处的级数展开：

使用 SeriesCoefficient 获取级数展开的通项：

应用 (3)

使用 FoxHReduce 可获取几乎任何数学函数关于 FoxH 的表示：

更少见的组合：

三项式根以 FoxH 表示的形式：

当时进行验证：

一般三项式的根也可表示为关于 FoxH 的形式：

当且时验证根：

用 FoxH 来表示 StableDistribution 的 PDF，即在的情况下：

对其进行计算并与使用 StableDistribution 生成的内置 PDF 进行比较：

属性和关系 (2)

FunctionExpand 返回函数关于 FoxH 的表示：

FoxHReduce 返回函数的 FoxH 表示：

可能存在的问题 (3)

是 FoxH 的奇点：

当参数为正且为正且精确时，原点处 Series 可用：

当参数为正且为正且精确时，Infinity 处的 Series 可用：

巧妙范例 (1)

许多初等和特殊函数是 FoxH 的特例：

顶部