FunctionPoles

FunctionPoles[f,x]

変数 x を持つ有理型関数 f の極を求める．

FunctionPoles[{f,cons},x]

x が制約条件 cons で制限されている際の f の極を与える．

詳細とオプション

  • 関数の極は極特異点としても知られている．
  • 関数の極は，複素解析における関数の留数の計算やベキ級数の収束半径の計算にしばしば使われる．
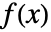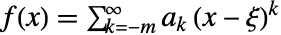  • 関数 は，の形の級数表現を持つのであれば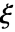， に多重度 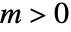の極特異点を持つ．関数が極特異点しか持たないなら，その関数は有理型である．
  • FunctionPolesは{pole,multiplicity}ペアのリストを返す．
  • 関数 f は制約条件 cons を満足する x について有理型でなければならない．
  • cons は，等式，不等式，これらの論理結合を含むことができる．
  • 次は，使用可能なオプションである．
  • Assumptions $Assumptionsパラメータについての仮定
    GeneratedParameters C生成されたパラメータの命名方法
    PerformanceGoal $PerformanceGoalスピードと品質のどちらを優先するか
  • FunctionPolesが多重度の特定に失敗した場合は，返された極の中に多重度がIndeterminateのものがあるかもしれない．

例題

すべて開くすべて閉じる

例  (2)

有理関数の極を求める：

極の集合は無限かもしれない：

スコープ  (6)

有理関数：

無限に多くの極がある関数：

TemplateBox[{x}, Abs]<=2のときの極を求める：

解析関数には極がない：

はに加除特異点を持つ：

FunctionPolesの入力関数は有理型でなければならない：

この関数はのとき有理型である：

多重度の決定に失敗した場合，返された極の中にはIndeterminateの多重度を持つものがあるかもしれない：

オプション  (3)

Assumptions  (1)

パラメータについての条件を指定する：

GeneratedParameters  (1)

FunctionPolesは，解を表すために新たなパラメータを導入することがある：

GeneratedParametersを使ってパラメータの命名方法を制御する：

PerformanceGoal  (1)

極の多重度の計算には時間がかかるかもしれない：

PerformanceGoal"Speed"とすると多重度の計算にかける時間が制限される：

どちらの場合も返される極は同じである：

最初の場合は，すべての多重度の計算に成功している：

2番目の場合は計算されていない多重度もある：

アプリケーション  (3)

有理型関数の特異点を分類する：

FunctionSingularitiesは極と加除特異点の場所を与える：

は に二重極を，に単一の極を，に加除特異点を持つ：

単位円に沿ってTemplateBox[{{{x, ^, 3}, -, {x, /, 3}}}, Gamma]を積分する：

単位円板上で の極を計算する：

留数定理を使って積分を計算する：

数値積分の結果と比較する：

におけるのテイラー(Taylor)級数の収束半径を求める：

収束半径は最も近い極までの距離に等しい：

たとえ極が複素数でも，実数上の収束に影響する：

はより極から遠いので，における収束半径の方が大きい：

特性と関係  (4)

極における関数の絶対値の極限はである：

Limitを使って極限を計算する：

多重度 の極における関数のベキ級数の最初の項の指数は である：

Seriesを使って級数を計算する：

Residueを使って指数がの級数項における係数を求める：

有理型関数が持ち得る唯一の特異点は極と加除特異点である：

FunctionSingularitiesを使ってすべての特異点によって満足される条件を求める：

SolveValuesを使って特異点を求める：

この関数はとに極を持ち，に加除特異点を持つ：

FunctionPolesを使って関数の極を求める：

Residueを使って極における留数を求める：

ResidueSumはすべての極における留数の和を与える：

考えられる問題  (2)

多重度の判定に失敗した場合は，返された極の中にIndeterminateの多重度を持つものがあるかもしれない：

FunctionPolesは非厳密入力を有理化し，結果を入力精度に近似する：

結果はどの有理数が選ばれたかに依存する：

最初の例では有理化された指数は整数だが2番目の例はそうではない：

Wolfram Research (2021), FunctionPoles, Wolfram言語関数， https://reference.wolfram.com/language/ref/FunctionPoles.html.

テキスト

Wolfram Research (2021), FunctionPoles, Wolfram言語関数， https://reference.wolfram.com/language/ref/FunctionPoles.html.

CMS

Wolfram Language. 2021. "FunctionPoles." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionPoles.html.

APA

Wolfram Language. (2021). FunctionPoles. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionPoles.html

BibTeX

@misc{reference.wolfram_2024_functionpoles, author="Wolfram Research", title="{FunctionPoles}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionPoles.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_functionpoles, organization={Wolfram Research}, title={FunctionPoles}, year={2021}, url={https://reference.wolfram.com/language/ref/FunctionPoles.html}, note=[Accessed: 18-November-2024 ]}